On this page, I’m talking about stoichiometry. Stoichiometry is a part of chemistry that is used to know how much of one of the species is produced or consumed to obtain other chemical species. This is based on balanced chemical equations (I have another page where I show how to balance chemical equations, click here to see it).
The outline for this page is:
Mol-to-mol calculations
In this type of problem, we are asked to calculate the number of moles necessary to produce or react given another number of moles of another species.
For example, the reaction with hydrogen with nitrogen to produce ammonia is:
N2 + 3H2 → 2NH3
We can be asked to find how many moles of hydrogen (H2) will react if we only have 0.25 mol of nitrogen (N2). I will explain 2 ways to solve this problem: using molar ratios and the factor label method (also called unit factor method or dimensional analysis). The mechanism of both methods is very similar and you can use whichever is easier for you.
Molar ratios
The given equation:
N2 + 3H2 → 2NH3
means that 1 mol of nitrogen reacts with 3 mol of hydrogen to produce 2 mol of ammonia. The balanced equation gives the molar ratios, in this example, we have the following molar ratios:
- N2:H2 = 1:3 (this is equivalent to H2: N2 = 3:1, don’t need to write twice)
- N2:NH3 = 1:3
- H2:NH3 = 3:2
This is equivalent to writing them in fractions, for example:
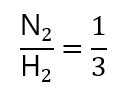
Coming to the problem: how many mols of hydrogen (H2) will react if we only have 0.25 mol of nitrogen (N2)? Note: as we are asked the number of moles of H2, I tend to put it first (or in the numerator) in the molar fraction, you can do in the other way round if you want, but I find easier in this way:
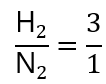
As we are given 0.25 mol N2, we call x the number of mol of H2 to find and express this ratio as:
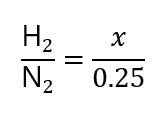
Therefore, we can say that:
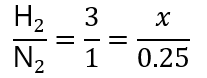
If we ignore the H2/N2, we get a mathematical equation that we can solve:
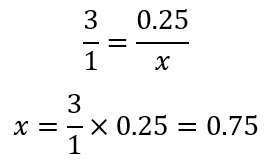
Factor label method
Factor label method (also called unit factor method or dimensional analysis) is a useful tool in science, and many problems can be solved with its aid, if you are not familiar with it, check it here. In this method, for the generic reaction:
aA + bB → cC + dD
where a, b, c and d are the respective coefficients of the chemical species A, B, C and D, we have equivalences like:
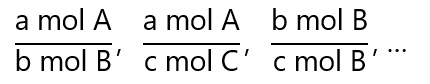
Let’s see solve the above example. How many mol of hydrogen (H2) will react if we only have 0.25 mol of nitrogen (N2)? The reaction is:
N2 + 3H2 → 2NH3
From the balanced chemical equation, we have the following proportion:
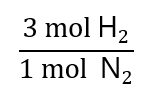
As we have 0.25 mol N2, we can write:
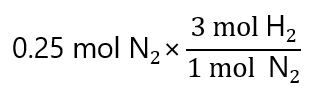
And ‘mol N2’ can be cancelled, as it appears in the numerator and denominator:
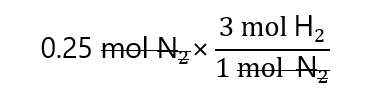
Obtaining:
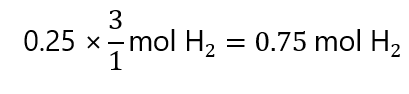
Molar ratio or factor label method? As you can see, both are similar and lead to the same answer. It is entirely up to you which one to use in each case. I use the factor label method here, as I find it more didactic and systematic.
Example 1
According to the following equation, how many mol of sodium hydrogen phosphate (Na2HPO4) can be prepared with 1.5 mol of sodium hydroxide (NaOH)?
2NaOH + H3PO4 → Na2HPO4
Note: there is no information about the phosphoric acid (H3PO4), so we can assume that there is enough to produce the reaction. Unless it is specified, we can assume that it is the case.
Answer
From the equation, we know that the proportion of Na2HPO4 and NaOH is:
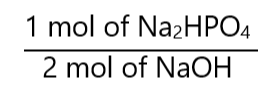
As we have 1.5 mol of NaOH, we can conclude that we can prepare:
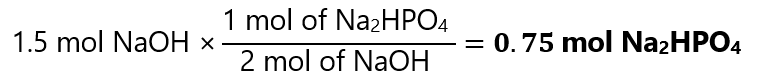
==========
Example 2
Phosphorous trichloride (PCl3) reacts with water to produce phosphorous acid (H3PO3) and hydrochloride gas (HCl). How many moles of HCl can be produced from 1.50 mol PCl3? The adjusted reaction is
PCl3 + 3H2O → H3PO3 + 3HCl
Answer
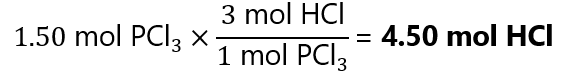
Calculations involving mass
These problems are similar to the previous ones, but instead of working with mols, we are working with mass. This will require converting mass to mol and vice versa. Remember that:
- to convert mass to mol we divide by the molecular mass
- To convert mol to mass, we multiply by the molecular mass.
Additionally, you can use the factor label method by expressing the molecular masses as:
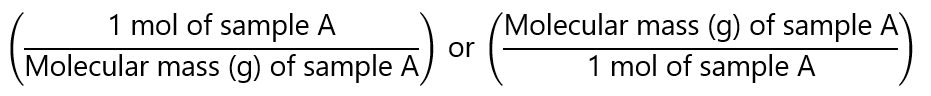
If you need a refresher about molecular masses, check my other page here. Once we have made the transformation, the problem can be solved as we have done in ‘mol-to-mol calculations’. For example, how many grams of ammonia (NH3) can we get if we have 9 g of hydrogen (H2) according to the following equation?
N2 + 3H2 → 2NH3
Atomic masses: H2: 2.016 g/mol, NH3: 17.031 g/mol
In the 1st step, we convert the grams of H2 to mols of H2 by dividing by its molecular mass:
9 g / 2.016 g/mol= 4.464 mol
Now the problem is like we have seen in mole-to-mol calculations: how many mols of N2 I get with 4.464 mol H2? The answer is:
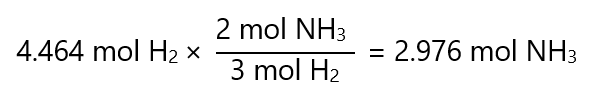
The final step is converting the 2.976 mol NH3 to grams of NH3 by multiplying by its molecular mass:

We could summarize all these steps in just one using the factor label method with the correspondent molecular masses (just be careful what go to the numerator and what go to the numerator):
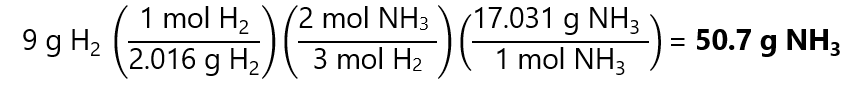
As you can see, the results are similar, but not the same due to rounding errors (errors that occur when you round a number to a few decimal places). Here, I will use both methods: using steps and summarizing all the steps in one using the factor label method. The steps are convenient when you start with these calculations, as you get more confident and know how to do it, try to do everything in one step using the factor label method, it is quicker and less prone to rounding errors.
Example 1
Propane (C3H8) burns following the reaction:
C3H8+5O2→4H2O+3CO2
If 250 g of C3H8 is burned, how many g of H2O is produced? Molecular masses: C3H8: 44 g/mol, H2O: 18 g/mol
- We convert the 250 g of C3H8 to mol of propane
250 g / (44 g/mol) = 5.68 mol
- As 1 mol C3H8 produces 4 mol of H2O, 5.68 mol of C3H8 produces:
5.68 mol C3H8 x (4 mol H2O / 1 mol C3H8) = 33.72 mol H20
- And 33.72 mol of H2O has a mass of:
33.72 mol x 18 g/mol = 408.96 g H2O.
Or in 1 step using the factor label method:
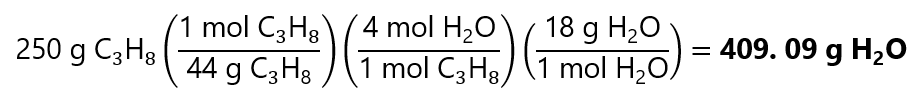
Discrepancy due to rounding errors: for example in step 1, the calculation 250/44 = 5.6818181818… and we have used only 5.68, these errors accumulate over the whole process. Both answers can be considered correct in most common situations. You can check repeating the step by step calculations but taking more decimals places, you will see that the number get closer to the value obtained with the factor label method.
Limiting quantities
In these types of problems, the amount of more than one reactant is given (either as mol, mass or a combination of mol and mass), one of the reactants is going to be completely consumed in the reactions, and the rest are going to be in excess. To solve a limiting quantities problem in which the reactant in excess is not obvious, use the following steps:
- Write the balanced equation of the reaction.
- If you have the masses of the reactants, convert them to mol (divide the masses by their molecular masses). If you have mol instead of masses, go to the next step.
- Calculate the molar ratio (proportions of the reactants) from the reaction and compare it with those provided. With the comparison, you will be able to find which is the limiting reactant. However, sometimes, having a look to the numbers in the molar ratios, it is not easy to see which one is in excess and which one is the limiting quantity. In these cases, divide the number of moles of each by the corresponding coefficient in the balanced chemical equation: the reagent with the lower quotient is the limiting quantity. These quotients are not used for any further calculations (if it is in an exam, cross them out as soon as you see which one is the limiting quantity).
Once you find the limiting reactant use stoichiometry with the limiting reactant to calculate the required values as we have done in the previous sections. If the molar ratio given is the same than in the adjusted reaction, all the reactants will be consumed on their totality, you only need to choose one of them for the calculations.
For example, if we have 2 mol of H2 and 2 mol of N2, how many mol of NH3 can we get?
Step 1: Write the balanced equation of the reaction.
N2 + 3H2 → 2NH3
Step 2: we already have the mol required. We go to the next step.
Step 3: compare the molar ratios:
From the equation, we have:
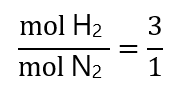
From those provided:
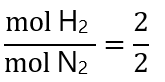
As the proportion of H2:N2 from the reaction is 3:1 and we have a proportion 1:1, the H2 is the limiting quantity (the 2 mol N2 requires 6 mol H2 and we only have only 2). However, if you don’t see it, let’s compare by dividing the number of mol given by their coefficients:
H2: 2/3 = 0.6…
N2: 2/1 = 2
As 0.6… < 2, the H2 is the limiting quantity.
To find how many mol of NH3 we can use the proportions from the equation:
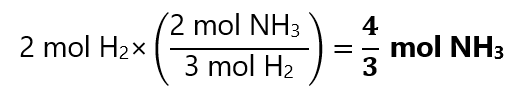
Example 1
90 g of sodium (Na) reacts with 80 g of sulfur (S) to produce sodium sulfide (Na2S). How many g of Na2S is obtained? How much of the reactant in excess is left? Molecular masses: Na: 23 g/mol, S: 32 g/mol
Answer
Step 1: write the balanced equation
2Na + S → Na2S
Step 2: Calculate the number of mol of each reactant:
Na: 92 g / 23 g/mol = 4 mol
S: 80 g/ 32 g/mol = 2.5 mol
Step 3: Calculate the molar ratios:
From the balanced equation: Na:S = 2:1
From the data given: Na:S = 4:2.5
Comparing the molar ratios, we can see that we have excess of S and the limiting reactant is the Na (2.5 mol of S requires 8 mol Na and we have only 4). Or if you prefer, dividing the number of mol given by their coefficients:
Na: 4/2 = 2
S: 2.5/1 = 2.5
Na is the limiting quantity.
To calculate how much Na2S we get is, we consider that the limiting reactant (Na) reacts completely:
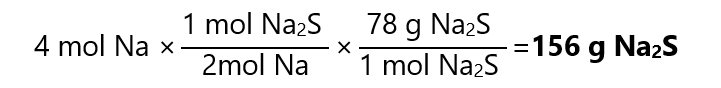
To calculate the S left without reaction, we can either use the law of the conservation of mass (as only 1 product is formed) or we can use the stoichiometry. I will explain both here, but usually, the law of the conservation of mass is more straightforward (as long as we have only 1 product, if it is not the case, use stoichiometry).
Ley the conservation of mass:
As 92 g of Na react completely to produce 156 g of Na2S, the difference in mass, 156 – 92 = 64 g is provided by the S. As we started with 80 g of S, we have left 80 g – 64 g = 16 g
Stoichiometry:
As we have produced 2 g of Na2S, from the stoichiometry of the reaction we have used
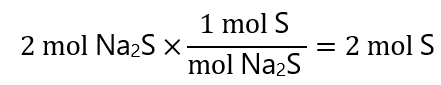
If we have used 64 g of S in the reaction and we started with 80 g of S, we have left 80 g – 64 g = 16 g.
As you can see, the stoichiometry and the law of conservation of mass give the same answer. This is not surprising, as the law of conservation of mass is at the core of mol and balancing equations.
==========
Example 2
How many grams of calcium perchlorate (Ca(CIO4)2) can be prepared by treatment of 12.5g calcium oxide (CaO) with 75.0 g perchloric acid (HClO4)? Atomic masses: CaO: 56.1 g/mol, HClO4: 100.5 g/mol, Ca(ClO2)4: 239/1 g/mol
Answer
Step 1: write the balanced equation
CaO + 2HCIO4 → Ca(ClO4)2 + H,O
Step 2: Calculate the mols of each reactant:
CaO: The number of mols is 12.5 g / 56.1 g/mol = 0.22 mol
HClO4: The number of mols is 75 g / 100.5 g/mol = 0.75 mol
Step 3: Calculate the molar ratios:
From the balanced equation: HCIO4:CaO = 2:1
From the data given: HCIO4:CaO = 0.75:0.22
As we can see, the limiting quantity is the CaO (for 0.22 mol CaO we need, 0.44 mol HclO4 and we have 0.75, more than we need). Or if you prefer, dividing the number of mol given by their coefficients:
HClO4: 0.75/2 = 0.375
CaO: 0.22/1 = 0.22
As 0.22 < 0.375, CaO is the limiting quantity. is the limiting quantity.
The mass of Ca(ClO4)2 obtained is:
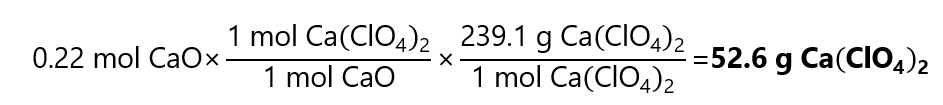
Exercises
Exercises: Mol-to-mol calculations
1. In the right conditions of pressure and temperature, nitrogen (N2) reacts with oxygen (O2) to produce nitric oxide (NO). How many mol of NO can be produced with 0.75 mol of N2 in excess of oxygen?
Answer
We start with the balanced equation:
N2 + O2 →2NO
From the equation, we can deduct that:
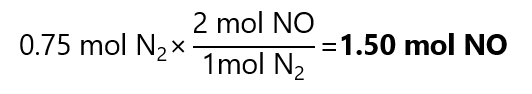
2. How many mol of water (H2O) are produced with the combustion of 5 mol of octane (C8H18).
Answer
Combustion reactions are reactions with oxygen. We start with the balanced chemical equation:
2C8H18 + 25O2 → 16CO2 + 18H2O
From the equation, we can deduct that:
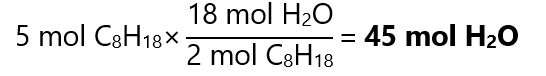
3. Phosphorus pentachloride (PCl5) reacts with water to produce phosphoric acid (H3PO4) and hydrochloric acid (HCl). How many mol of each acid can be obtained with 0.25 mol of PCl5?
Answer
We start by writing the balanced equation:
PCl5 + 4H2O → H3PO4 + 5HCl
From the equation, we can find that the H3PO4 formed is:

Similarly, the HCl formed is:

4. Barium hydroxide (Ba(OH)2) is neutralized with hydrobromic acid (HBr) to produce barium bromide (BaBr2). How many mol of HBr are required to form 0.75 mol of BaBr2.
Answer
From the balanced equation:
Ba(OH)2 + 2HBr → BaBr2 + 2H2O
We can find that need:
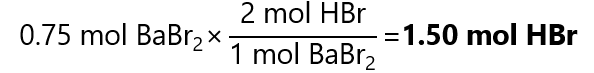
5. Phosphoric acid (H3PO4) neutralize sodium hydroxide (NaOH) to produce sodium phosphate (Na3PO4) and water. How many mol of sodium hydroxide are required to produce 0.2 mol of sodium phosphate?
Answer
From the balanced equation:
H3PO4 + 3NaOH → Na3PO4 + 3H2O
We get:
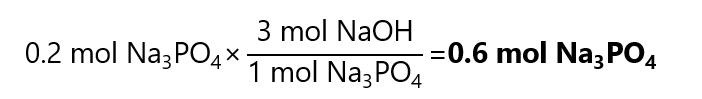
Exercises: Calculations involving masses
1. Sulfurous acid (H2SO3) reacts with sodium hydroxide (NaOH) to produce sodium sulfite (Na2SO3) and water. If we have 75.0 g of sulfurous acid:
a) how many grams of sodium hydroxide we need to react with the sulfurous acid?
b) How many grams of sodium sulfite will be produced?
Molecular masses: H2SO3: 82.0 g/mol, NaOH: 40.0 g/mol, Na2SO3: 126.0 g/mol
Answer
We start with the balanced chemical equation:
H2SO3 + 2NaOH → Na2SO3 + 2H2O
We then convert the mass of H2SO3 to mol with its molecular mass:
Number of mol: 75.0 g / (82.0 g/mol) = 0.915 mol H2SO3
To calculate the grams of NaOH required, first, we need to find how many mol NaOH will react with 0.915 mol H2SO3, we, then, calculate the mass of these mol. In steps:
First, from the equation, we can see that:
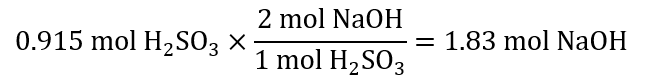
Second, to transform these 1.83 mol NaOH in g of NaOH, we multiply by its molecular mass:
1.83 mol x (40.0 g/mol) = 73.2 g of NaOH
Or in 1 step with factor label method:
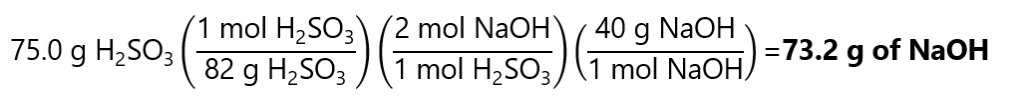
To calculate the grams of Na2SO3 produced, we proceed in similar manner than for the NaOH. First, we need to find how many mols of Na2SO3 will be produced by 0.915 mols of H2SO3, we, then, calculate the mass of these mols. In steps:
First, from the equation, we can see that:
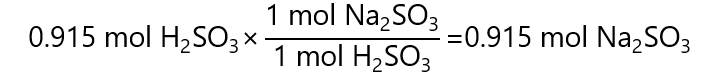
Second, to transform these 0.915 mol Na2SO3 in g, we multiply by its molecular mass:
0.915 mol x (126.0 g/mol) = 115.3 g of Na2SO3
Or in 1 step with factor label method:
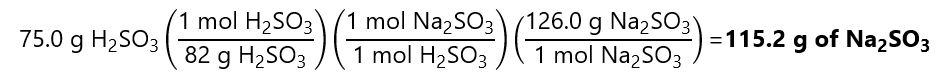
Discrepancy due to rounding errors.
2. How many grams of CO2 are produced in the combustion of 100.0 g of ethane (C2H6). Molecular masses: C2H6: 30.0 g/mol, CO2: 44.0 g/mol.
Answer
We start with the balanced chemical equation:
2C2H6 + 7O2 → 4CO2 + 6H2O
First, transform from g of C2H6 to mol of C2H6 by dividing by its molecular mass.
100.0 g / (30.0 g/mol) = 3.33 mol
Second, we calculate the number of mol of CO2 produced by 3.33 mol of C2H6. From the balanced chemical equation we obtain:
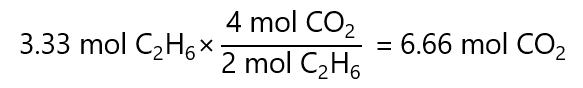
Third, we transform the 6.66 mols of CO2 obtained by multiplying by its molecular mass:
6.66 mol x 44.0 g/mol = 293.0 g of CO2.
Or using factor label method:
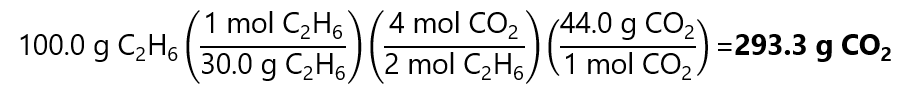
Difference in result due to rounding errors.
3. In industrial processes, phosphorus (P) is obtained in electric arc furnaces according to the equation:
2Ca3(PO4)2 + 6SiO2 + 10C → 6CaSiO3 + 10CO + P4
How many grams of Calcium Phosphate (Ca3(PO4)2) and silica (SiO2) are required to produced 1,000 g of tetra phosphorus (P4)?
Molecular masses: P4: 124.0 g/mol, Ca3(PO4)2: 310.3 g/mol, (SiO2) = 60.1 g/mol
Answer
We start by converting 1,000.0 g of P4 into mols by dividing by its molecular mass:
1,000 g / (124.0 g/mol) = 8.06 mol
To calculate the grams of Ca3(PO4)2 requires, we check how many mols of Ca3(PO4)2 are required to produce 8.06 mol P4 using the balanced chemical equation and convert that number to grams by multiplying by its molecular mass:
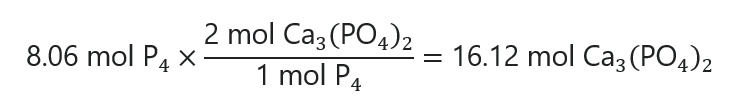
16.12 mol x 310.3 g/mol = 5002 g Ca3(PO4)2
Or doing all in one step using the factor label model:
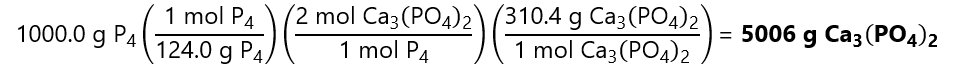
Difference in result due to rounding errors.
The same steps are followed for the SiO2:
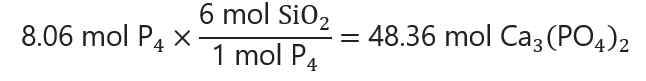
48.36 mol x 60.1 g/mol = 2,906 g SiO2
Or doing all in one step using the factor label model:
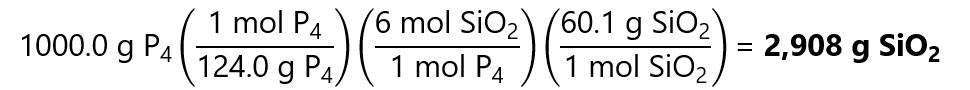
Difference in results due to rounding errors.
4. One method to produce sodium hydroxide (NaOH) is by treating sodium carbonate (Na2CO3) with calcium hydroxide (Ca(OH)2) according to the following balanced chemical equation:
Na2CO3 + Ca(OH)2 → CaCO3 + 2NaOH
How many grams of Na2CO3 we need to obtain 1,000.0 g of NaOH?
Molecular masses: NaOH: 40.0 g/mol, Na2CO3: 106.0 g/mol.
Answer
We transform 1,000.0 g of NaOH to moles by dividing by its molecular mass:
1,000.0 g / (40.0 g/mol) = 25 mol NaOH
Next, we calculate the number of moles of Na2CO3 that we need to react with 25 mol NaOH:
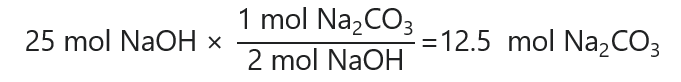
Finally, we convert 12.5 mol Na2CO3 in g multiplying by its molecular mass:
12.5 mol Na2CO3 x 106.0 g/mol = 1325.0 g Na2CO3
Or in 1 step using the factor label model:
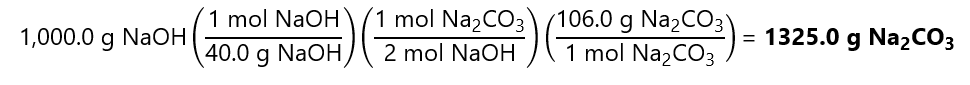
5. How many grams of sodium chloride (NaCl) can be obtained when 100.0 g of chlorine (Cl2) reacts with sodium (Na) according to the balanced chemical equation:
2Na + Cl2 → 2NaCl
Molecular masses: Cl2: 71.0 g/mol, NaCl: 58.5 g/mol
Answer
100.0 g of Cl2 is
100.0 g / (71.0 g/mol) = 1.41 mol Cl2.
1.41 mol Cl2 will produce:
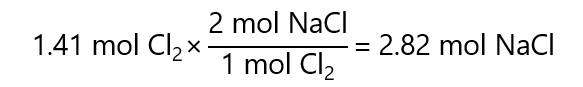
That multiply by the formula mass of NaCl, give the mass:
2.82 mol x 58.5 g/mol = 165.0 g of NaCl
Or in 1 step using the factor label model:
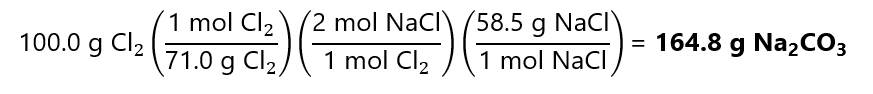
Difference in results duet rounding errors.
6. Barium hydroxide (Ba(OH)2) reacts with hydrochloric acid (HCl) to produce barium chloride (BaCl2) and water. How many grams of Ba(OH)2 and HCl will be required to produce 100.0 g of BaCl2?
Molecular masses: BaCl2: 208.3 g/mol, Ba(OH)2: = 171.3 g/mol, HCl: 36.5 g/mol.
Answer
The balanced chemical equation is:
Ba(OH)2 + 2HCl → BaCl2 + 2H2O
To obtain the number of moles of 100.0 g of BaCl2, we divide by its molecular mass:
100.0 g / (208.3 g/mol) = 0.48 mol BaCl2
To obtain the grams of Ba(OH)2, we start by checking how many moles of Ba(OH)2 are needed to form 0.48 mol BaCl2:
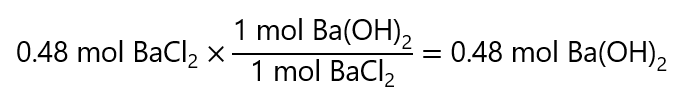
And we calculate the mass by multiplying by its molecular mass:
0.48 mol x 171.3 g/mol = 82.2 g Ba(OH)2
Or in 1 step using the factor label model:
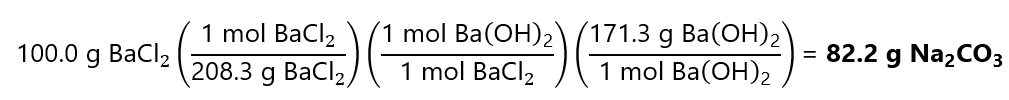
To calculate the grams of HCl required, we follow the same procedure: we start by checking how many moles of HCl are needed to form 0.48 mol BaCl2:
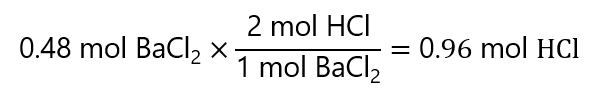
And we calculate the mass by multiplying by its molecular mass:
0.96 mol x 36.5 g/mol = 35.0 g HCl
Alternatively, in 1 step using the factor label model:
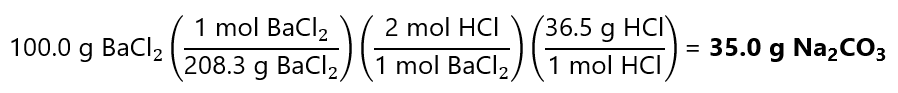
Note that we have used 82.2 g of Ba(OH)2 and 35.0 g of HCl (a total of 82.2 + 35.0 = 117.2 g) to obtain 100.0 g of BaCl2. Where are the 17.2 g left? It formed water. If you do the calculations, you will get this number (considering the rounding errors): we formed 0.96 mol H2O and its molecular mass is 18.0 g/mol.
7. How many grams of calcium chloride (CaCl2) are required to produce 50.0 g of silver chloride (AgCl) following the equation:
CaCl2 + 2AgNO3 → 2AgCl + Ca(NO3)2
Molecular masses: CaCl2: 111.0 g/mol, AgCl: 143.3 g/mol
Answer
The number of moles in 50.0 g of AgCl is:
50.0 g / (143.3 g/mol) = 0.3489 mol AgCl
(as the numbers are small, I take more decimal places to reduce rounding errors) 0.3489 mol AgCl require:

0.18 mol CaCl2 is
0.1745 mol x 111.0 g/mol = 19.4 g CaCl2
Or summarized in 1 step using the factor label method:
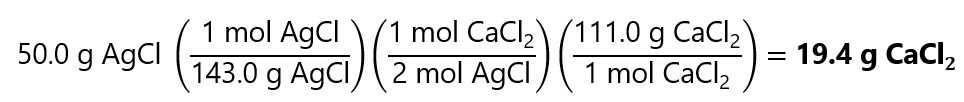
8. How many grams of calcium oxide (CaO) reacts with 7.0 g of hydrochloric acid (HCl) to produce calcium chloride (CaCl2) and water?
Molecular masses: CaO: 56.0 g/mol. HCl: 36.5 g/mol.
Answer
The adjusted chemical equation is:
CaO + 2HCl → CaCl2 + H2O
Dividing 7.0 g of HCl by its molecular mass, we get the number of moles:
7.0 g / (36.5 g/mol) = 0.1917 mol HCl
0.1917 mol HCl react with:
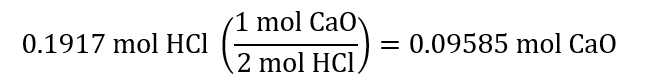
0.09585 mol CaO is:
0.09585 x 56.0 g/mol = 5.4 g of CaO
If you prefer, in 1 step using the factor label method:
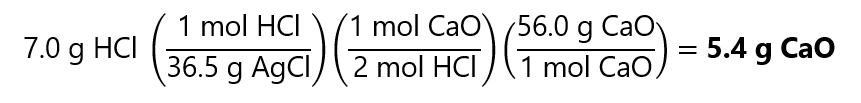
9. Iron (Fe) is oxidised to produce iron (III) oxide (Fe2O3) according to the reaction:
4Fe + 3O2 → 2Fe2O3
How many grams of Fe2O3 will be obtained with 100.0 g of Fe?
Molecular mass Fe2O3: 159.7 g/mol. Atomic mass Fe: 55.8 g/mol.
Answer
100.0 g of Fe is:
100.0 g / (55.8 g/mol) = 1.792 mol Fe
From the reaction, we know that 1.792 mol Fe will form:
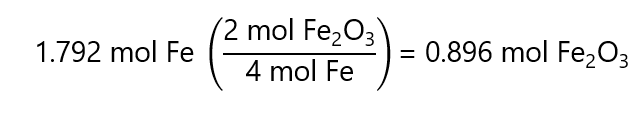
0.896 mol Fe2O3 is:
0.896 mol x 159.7 g/mol = 143.1 g Fe2O3.
Or solving the problem in 1 step using the factor label method:
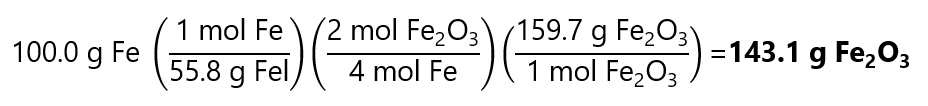
10. Nitrogen chloride (NaCl3) is hydrolysed by hot water to release ammonia (NH3) and hypochlorous acid (HOCl):
NCl3 + 3H2O → NH3 + 3HOCl
How many grams of NH3 can be produced from 25.0 g of NaCl3
Molecular masses: NaCl3: 120.4 g/mol, NH3: 17.0 g/mol
Answer
25.0 g of NaCl3 is:
25.0 g / (120.4 g/mol) = 0.2076 mol NaCl3
0.2076 mol NaCl3 forms:
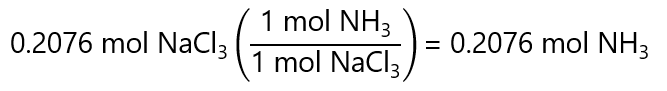
Or 1 in step using the factor label method:
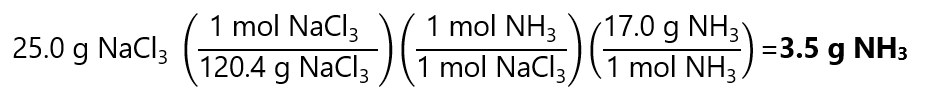
Exercises: Limiting quantities
1. How many grams of sodium choride (NaCl) can be obtained with 5 moles of sodium (Na) and 8 moles of chlorine (Cl2) according to the balanced chemical equation:
2Na + Cl2 → 2NaCl
Molecular mass: NaCl: 58.4 g/mol
Answer
The first step is to check whether we have a limiting quantity.
The molar ratio of the equation is Na:Cl2 = 2:1
The molar ratio of the given reactants is Na:Cl2 = 5:8
We can see that the limiting quantity is the Na, as we will need (8 x 2 =) 16 mol Na to react with all Cl2, but we only have 5. Or if we divide the number of mol given by their coefficients:
Na: 5/2 = 2.5
Cl2: 8/1 = 8
As 2.5 < 8, Na is the limiting quantity
As the Na is the limiting factor we can form:
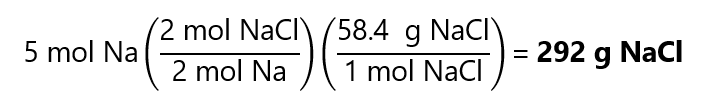
2. Calculate the number of grams of much carbon tetrachloride (CCl4) that can be produced with 10.0 g of carbon (C) and 100.0 g of chlorine (Cl2) according to the following equation:
C + 2Cl2 → CCl4
Molecular masses: C: 12.0 g/mol, Cl2: 70.9 g/mol, CCl4: 153.8 g/mol.
Answer
We start checking the number of moles of C and Cl2 provided:
C: 10.0 g / (12.0 g/mol) = 0.833 mol C
Cl2: 100.0 g / (70.9 g/mol) = 1.410 mol Cl2
From the balanced chemical formula, we have a molar ratio Cl2:C = 2:1
From the reactants supplied, we have a molar ration Cl2:C = 1.410: 0.833
We can see that the Cl2 is limiting quantity (we would need (2 x 1.410 =) 1.666 moles of Cl2 and we only have 1.410). Alternatively, dividing the number of mol given by their coefficients:
Cl2: 1.410/2 = 0.705
N2: 0.833/1 = 0.833
As 0.705 < 0.833, Cl2 is the limiting quantity.
We solve the problem as we did in the previous section (in this section I will be using the the factor label method instead of going step by step, you can go step by step and we should have similar results. If it is not the case, feel free to leave a comment):
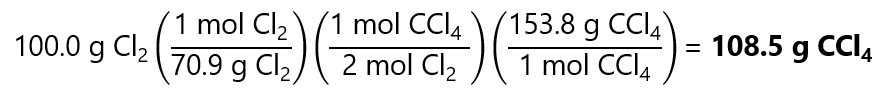
3. How many grams of potassium sulfate (K2SO4) will be obtained if 10.0 g of sulfuric acid (H2SO4) are mixed with 20.0 g of potassium hydroxide (K(OH))? The adjusted reaction is:
H2SO4 + 2KOH → K2SO4 + 2H2O
Molecular masses: H2SO4: 98.1 g/mol, KOH: 56.1 g/mol, K2SO4: 174.3 g/mol
Answer
We start by calculating the number of moles of H2SO4 and KOH we have:
H2SO4: 10.0 g / (98.1 g/mol) = 0.102 mol H2SO4
KOH: 20.0 g / (56.1 g/mol) = 0.356 mol KOH
The molar ratios are:
The molar ratio of the reaction is KOH: H2SO4 = 2:1
The molar ratio of the reactants given are: KOH: H2SO4 = 0.356:0.102 (~3.5:1)
As you can see, from the molar ratios. If you are not sure, divide the number of moles by their coefficients:
KOH: 0.356/2 = 0.178
H2SO4: 0.102/1 = 0.102
As 0.102 < 0.178, H2SO4 is the limiting quantity.
The grams of K2SO4 that we will obtain is:
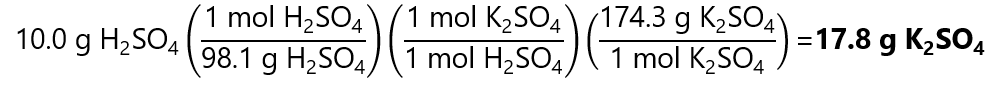
4. How many grams of iron (III) hydroxide (Fe(OH)3) we get when to 25.0 grams of FeCl3 and we add 15.0 grams of NaOH. The reaction is:
FeCl3 + 3NaOH → Fe(OH)3 + 3NaCl
Molecular weights: FeCl3: 162.2 g/mol, NaOH: 40.0 g/mol, Fe(OH)3: 106.9 g/mol
Answer
The number of moles of FeCl3 and NaOH are:
FeCl3: 25.0 g / 162.20 g/mol = 0.154 mol FeCl3
NaOH: 15.0 g / 40.0 g/mol = 0.375 mol NaOH
The molar ratios are:
The molar ratio of the reaction NaOH:FeCl3 = 3:1
The molar ration given NaOH:FeCl3 = 0.375:0.154
As we will need (3 x 0.154 =) 0.462 mol NaOH to react with FeCl3 and we only have 0.375 mol, NaOH is the limiting quantity. Or dividing the number of mol by their coefficients:
NaOH: 0.375/3 = 0.125
FeCl3: 0.154/1 = 0.154
As 0.125 < 0.154, NaOH is the limiting quantity.
Therefore, we get:
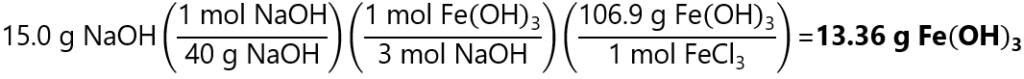
5. How many grams of calcium phosphate (Ca3(PO4)2) can be made by the reaction of 10.0 g calcium chloride (CaCl2) and 8.0 g potassium phosphate (K3PO4)? The reaction is:
3CaCl2 + 2K3PO4 → Ca3(PO4)2 + 6KCl
Molecular masses: Ca3(PO4)2: 310.2 g/mol, CaCl2: 110.98 g/mol, K3PO4: 212.27 g/mol
Answer
First, let’s calculate the number of moles of CaCl2 and K3PO4 available:
CaCl2: 10.0 g / 1110.98 g/mol = 0.090 mol
K3PO4: 8.0 g / 212.27 g/mol = 0.038 mol
Then we calculate if any reactant is in excess by checking the molar ratio:
Molar ration from reaction: CaCl2:K3PO4 = 3:2
From the reactants given: CaCl2:K3PO4 = 0.090:0.038
In this case, it seems easy to transform the molar ratio to numbers to divide the number of moles by their coefficients to find the limiting quantity:
CaCl2: 0.090/3 = 0.030
K3PO4: 0.038/2 = 0.019
As 0.019 < 0.030, K3PO4 is the limiting quantity. We obtain:
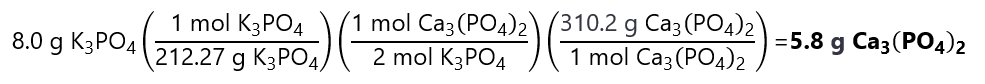
6. How many grams of aluminum oxide (Al2O3) can be obtaining by reacting 124 g of aluminum (Al) and 134 g of oxygen (O2)? The balanced chemical reaction is:
4Al + 3O2 → 2Al2O3
Molecular masses: Al: 26.98 g/mol, O2: 31.998 g/mol, Al2O3: 101.96 g/mol
Answer
The number of mol of Al and O2 are:
Al: 124 g / (26.98 g/mol) = 4.594 mol
O2: 134 g / (31.998 g/mol) = 4.188 mol
Comparing the molar ratios:
The molar ratio from the reaction is Al:O2 = 4:3 (i.e. we need more Al).
The molar ratio given is Al:O2 4.594: 4.188 (close to 1:1, well not exactly, but it helps us to decide)
Comparing the molar ratio, we can decide that the Al is the limiting quantity. If we are still not sure, we divide the number of moles by the coefficients to obtain:
Al: 4.594/4 = 1.1485
O2: 4.188/3 = 1.396
As 1.1485 < 1.396, Al is the limiting quantity. The number of mol Al2O3 that we get is:
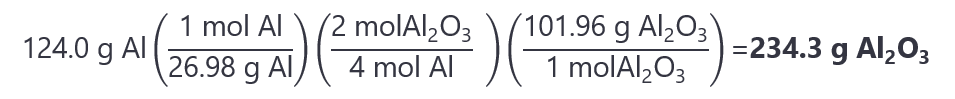
7. If 12.0 g of calcium oxide (CaO) is treated with 102.0 g of perchloric acid (HClO4), how many grams of calcium perchlorate (Ca(ClO4)2) are obtained? Adjusted reaction:
CaO + 2HClO4 → Ca(ClO4)2 + H2O
Molecular masses: CaO: 56.08 g/mol, HClO4: 100.46 g/mol, Ca(ClO4)2: 239.1 g/mol.
Answer
The moles of CaO and HClO4 are:
CaO = 12.0 g / 56.08 g/mol = 0.214 mol
HClO4 = 102.0 g / 100.46 g/mol = 1.015 mol
The molar ratios are:
From the reaction is HClO4:CaO = 2:1.
Given is is HClO4:CaO = 1.015:0.214 (~5:1),
Therefore the CaO is the limiting quantity. If you still are not sure, divide the number of moles given by their coefficients:
CaO: 0.214/1 = 0.214
HClO4: 1.015/2 = 0.508
As 0.214 < 0.508, CaO is the limiting quantity.
The moles of Ca(ClO4)2 obtained are:
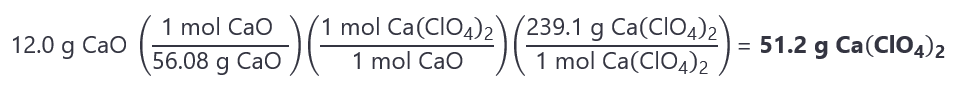
8. How many grams of lead II chloride (PbCl2) are produced from the reaction of 20.0 g of sodium chloride (NaCl) and 70.0 g of lead(II) nitrate (Pb(NO3)2)? Adjusted reaction:
2NaCl + Pb(NO3)2 → 2NaNO3 + PbCl2
Molecular masses: NaCl: 58.44 g/mol, Pb(NO3)2: 331.2 g/mol, PbCl2: 278.1 g/mol.
Answer
The moles of NaCl and Pb(NO3)2 that we have are:
NaCl: 20.0 g / 58.44 g/mol = 0.342 mol
Pb(NO3)2: 70.0 g / 331.2 g/mol = 0.211 mol
The molar ratios are:
Reaction NaCl:Pb(NO3)2 = 2:1
Given: NaCl:Pb(NO3)2 = 0.342:0.211.
We can see that the NaCl is the limiting quantity, as we will need (0.211 x 2 =) 0.422 mol and we only have 0.342. If you prefer to see it by dividing the number of mol by their coefficient, we have:
NaCl: 0.342 / 2 = 0.171
Pb(NO3)2: 0.422 / 1 = 0.422
As 0.171 < 0.422, the NaCl is the limiting quantity.
The mass of PbCl2 that we get is:
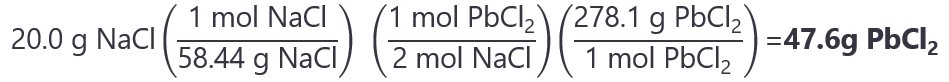
9. How many grams of iron (Fe) is formed when 80.0 g of iron (III) oxide (Fe2O3) reacts with 40.0 g of aluminium (Al)? Balanced reaction:
Fe2O3 + 2Al → 2Fe + Al2O3
Molar masses: Fe2O3: 159.690 g/mol, Al: 26.982 g/mol, Fe: 55.845 g/mol.
Answer
We start by checking how many mol of Fe2O3 and Al we have:
Fe2O3: 80.0 g / 159.690 g/mol = 0.501 mol Fe2O3
Al: 40.0 g / 26.982 g/mol = 1.482 mol Al
The molar ratios are:
From the reaction is Al:Fe2O3 = 2:1
Given Al:Fe2O3 = 1.482:0.501
We can see that we need (0.501 x 2 =) 1.002 mol of Al to react with the 0.501 mol of Fe, and we have 1.482, the Al is in excess and the Fe2O3 is the limiting quantity. This can be confirmed by dividing the number of moles by their coefficients:
Fe2O3: 0.501 / 1 = 0.501
Cl: 1.482/ 2 = 0.741
As 0.501 < 0.741, Fe2O3 is the limiting quantity. The mass of Fe we get is:
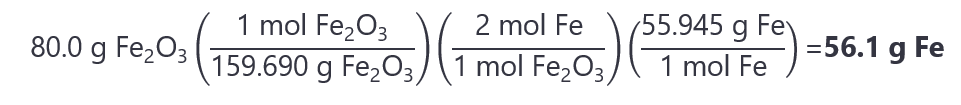
10. Calculate the grams of copper (II) nitrate (Cu(NO3)2) are obtained when 20.0 g of copper (II) chloride (CuCl2) reacts with 15.0 g sodium nitrate (NaNO3) as per the following equation:
CuCl2 + 2NaNO3 → Cu(NO3)2 + 2NaCl
Molecular masses: CuCl2: 134.45 g/mol, NaNO3: 84.995 g/mol, Cu(NO3)2: 187.56 g/mol.
Answer
The number of mol of CuCl2 and NaNO3 given are:
CuCl2: 20.0 g / 134.45 g/mol = 0.149 mol CuCl2
NaNO3: 15.0 g / 84.995 g/mol = 0.176 mol NaNO3
The molar ratios are:
Reaction is NaNO3:CuCl2 = 2:1
Given: NaNO3:CuCl2: 0.176:0.149 (~1:1)
We can see that the limiting quantity is the NaNO3, as we need (0.176 x 2 =) 0.352 mol and we only have 0.176 mol. You can always divide the number of mol by their coefficients:
NaNO3: 0.176 / 2 = 0.088
CuCl2: 0.149 / 1 = 0.149
As 0.088 < 0.149, the NaNO3 is the limiting quantity.
The mass of Cu(NO3)2 obtained is:
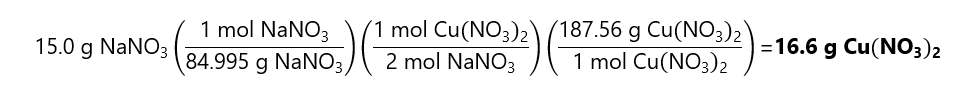
11. Calculate the mass of zinc oxide (ZnO) when 20.0 g of zinc (Zn) is heated with 20.0 g of molybdenum trioxide (MoO3) as per the reaction:
3Zn + 2MoO3 → Mo2O3 + 3 ZnO
Molecular masses: Zn: 65.38 g/mol, MoO3: 143.94 g/mol, ZnO: 81.38 g/mol
Answer
The moles of Zn and MoO3 that we have are:
Zn: 20.0 g / 65.38 g/mol = 0.306 mol ZnO
MoO3: 20.0 / 143.94 g/mol = 0.139 mol MoO3
The molar ratios are:
From the reaction: Zn:MoO3 = 3:2
From the reactants given: Zn:MoO3 = 0.306:0.139, it is ~3:1
Therefore the limiting quantity is the MoO3. We can confirm it by dividing the number of mol by their coefficients:
Zn: 0.306 / 3 = 0.102
MoO3: 0.139 / 2 = 0.069
As MoO3 gives a lower value, it is the limiting quantity. The grams of ZnO obtained is:

Comments
If you have any question, or want to add anything else, please leave a comment below.
