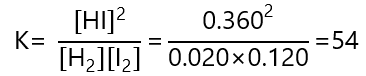On this page, we delve into the fascinating concept of chemical equilibrium. Here, we explore how this equilibrium can be shifted and uncover methods to determine the concentrations of various species within the equilibrium state.
The outline for this page is
1. Chemical equilibrium and Le Chatelier principle
3. Exercises
4. Comments
Chemical equilibrium and Le Chatelier principle
Many chemical reactions convert practically all the reactant(s) (or the limiting quantity). In other reactions, when the products are formed, they react to form the original reactants again, leading to a situation in which we have some products and reactants together with no sign of the reaction occurring. We are in a situation where we have two opposite reactions occurring at the same time, this is called chemical equilibrium. For example, in the process of producing ammonia (NH3) via the Haber process, we have 2 competing reactions: the formation of ammonia from nitrogen (N2) and hydrogen (H2):
N2 + 3H2 → 2NH3
And the decomposition of the NH3 into N2 and H2:
2NH3 → N2 + 3H2
In these cases, we write a reaction with a double arrow (⇄):
N2 + 3H2 ⇄ 2NH3
The convention of calling reactants to the substances on the left and products on the right still applies (yes, I know, the reaction happens in both ways, but it is the convention and it helps when we refer to the equation).
When a reaction reaches equilibrium, no change is observed, it doesn’t mean that the reaction has stopped, in reality, both reactions are happening at the same time with no net change happening. However, we can change the equilibrium if we change the conditions, this is known as the Le Chatelier principle:
When a simple system in thermodynamic equilibrium is subjected to a change in concentration, temperature, volume, or pressure, (1) the system changes to a new equilibrium, and (2) this change partly counteracts the applied change.
We are going to see how the principle is applied to the reaction
N2 + 3H2 ⇄ 2NH3
Effect of concentration
When there is an increase in the concentration of any of the reactants or products involved in the equilibrium, the equilibrium will respond by shifting in an attempt to counteract and minimize the impact of that concentration change.
For example, in the reaction
N2 + 3H2 ⇄ 2NH3
The addition of hydrogen will increase its concentration, to keep the equilibrium, the system will tend to reduce the hydrogen by producing more ammonia and shifting the equilibrium to the right.
Effect of temperature
The effect of temperature can be easily checked by adding the word ‘heat’ to the reaction:
* If the reaction [left to right] is exothermic (produces heat or increases the temperature), we add heat as a product
aA + bB ⇄ cC + dD + Heat
* If the reaction [left to right] is endothermic (reduces heat or decreases the temperature), we add heat as a reactant
aA + bB + Heat ⇄ cC + dD
The reaction of the formation of ammonia via the Harber process is exothermic (produces heat), so we can write:
N2 + 3H2 ⇄ 2NH3 + heat
What will happen if we heat the system? The system will try to reduce the heat and will use the heat added to decompose ammonia, shifting to the left. For the same principle, if we reduce the temperature of the system, the equilibrium will shift to the right, producing more ammonia.
Effect of the pressure
The impact of pressure varies significantly between gases, liquids, and solids within a system. Therefore, when investigating the effect of pressure on a reaction, we focus primarily on the substances in the gas state. In the given system:
N2(g) + 3H2(g) ⇄ 2NH3(g)
All the substances exist as gases. The reactants consist of 4 moles of gases (1 mole from N2 and 3 moles from H2), while the products contain 2 moles of gases. If pressure increases, the system will respond by counteracting the change to maintain equilibrium. This means reducing the pressure, which is achieved by decreasing the volume through the reduction of gas moles in the system. Consequently, the system will shift to the right, leading to an increase in NH3 production while reducing the amounts of H2 and N2. Conversely, a decrease in pressure will cause NH3 to decompose.
Presence of a catalyst
The addition of a catalyst does not affect the equilibrium, it just speeds up forward and backward reactions, reaching the equilibrium faster.
Equilibrium constants
Le Chatelier does not tell us how much equilibrium is shifted. We can find the position of the equilibrium using the equilibrium constant. Once the equilibrium is reached at the given pressure and temperature for the generic reaction
aA +bB ⇄ cC + dD
where A, B, C and D are chemical species and a, b, c and d are their respective coefficients, we define the equilibrium constant as:
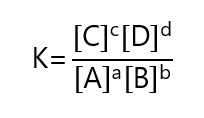
Where [A], [B], [C] and [D] are the molar concentrations in equilibrium of A, B, C and D respectively.
For example, given the equation:
N2 + 3H2 ⇄ 2NH3
The equilibrium constant is given by:
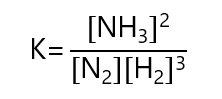
Example 1
Calculate the equilibrium constant of the reaction
A + B ⇄ C +D
If at equilibrium the concentration of A is 0.50 M, B is 0.40 M, C is 0.30 M and D is 0.45 M?
Answer
Replacing the numbers in the equation:
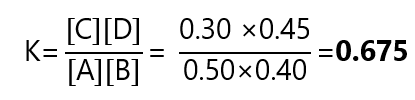
Example 2
A solution containing 1.50 M of A and 2.50 M of B is allowed to reach equilibrium. At equilibrium, the concentration of C is 0.50 M. Calculate the equilibrium constant if the reaction is:
A + B ⇄ C +D
Answer
In the exercises where we have to find the concentrations in equilibrium, it is better if we go systematically step by step, checking:
-
- Initial concentrations
-
- Changes of each concentration produced by the reaction
-
- Concentrations at equilibrium
(You can remember by ICE: Initial, Changes and Equilibrium)
We start with the initial concentrations, from the wording of the exercise, we can consider that we don’t have C or D, therefore we can write:
A + B ⇄ C +D
| [A] | [B] | [C] | [D] | |
| Initial | 1.50 | 2.50 | 0.00 | 0.00 |
| Change | ||||
| Equilibrium |
From the wording, we know that the in the equilibrium, we have a concentration 0.50 M of C:
A + B ⇄ C +D
| [A] | [B] | [C] | [D] | |
| Initial | 1.50 | 2.50 | 0.00 | 0.00 |
| Change | ||||
| Equilibrium | 0.50 |
Checking the stoichiometry of the reaction, for each mol of C produced, we also produce 1 mol of D and we use 1 mol of A and 1 mol of B, therefore, we can update the table as:
A + B ⇄ C +D
| [A] | [B] | [C] | [D] | |
| Initial | 1.50 | 2.50 | 0.00 | 0.00 |
| Change | -0.50 | -0.50 | +0.50 | +0.50 |
| Equilibrium | 0.50 |
We just need to add the 2 first rows into the empty cells of the third row
A + B ⇄ C +D
| [A] | [B] | [C] | [D] | |
| Initial | 1.50 | 2.50 | 0.00 | 0.00 |
| Change | -0.50 | -0.50 | +0.50 | +0.50 |
| Equilibrium | 1.00 | 2.00 | 0.50 | 0.50 |
And calculate the value of K:
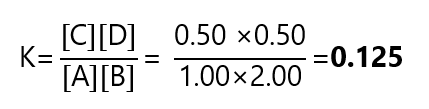
Example 3
Calculate the equilibrium constant of example 2 if the reaction is given by
2A + B ⇄ C +D
Answer
We can follow the previous example to write the initial concentrations and the concentration of C:
2A + B ⇄ C +D
| [A] | [B] | [C] | [D] | |
| Initial | 1.50 | 2.50 | 0.00 | 0.00 |
| Change | ||||
| Equilibrium | 0.50 |
As the stoichiometry of the reaction has changed, we need to amend the changes by reaction: B, C and D are unchanged from the previous example (for each mol of C produced, we also produce 1 mol of D and we use 1 mol of B). A is different now: for every mol of C formed, we have consumed 2 moles of A therefore, if we have formed 0.5 moles of C, we have consumed 0.5 moles of A, using the factor label method:

2A + B ⇄ C +D
| [A] | [B] | [C] | [D] | |
| Initial | 1.50 | 2.50 | 0.00 | 0.00 |
| Change | -1.00 | -0.50 | 0.50 | 0.50 |
| Equilibrium | 0.50 |
We just need to add the 2 first rows into the empty cells of the third row
2A + B ⇄ C +D
| [A] | [B] | [C] | [D] | |
| Initial | 1.50 | 2.50 | 0.00 | 0.00 |
| Change | -1.00 | -0.50 | +0.50 | +0.50 |
| Equilibrium | 0.50 | 2.00 | 0.50 | 0.50 |
And calculate the value of K:
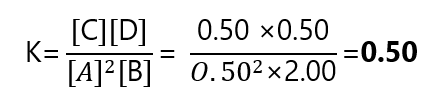
Example 4
Given the reaction:
A + B ⇄ C +D
With an equilibrium constant 0.10. What are the concentrations in equilibrium if the initial concentrations were 1.25 M of A and 1.50 M of B?
Answer
We start with the initial concentrations, from the wording of the exercise, we can consider that we don’t have C or D, therefore we can write:
A + B ⇄ C +D
| [A] | [B] | [C] | [D] | |
| Initial | 1.25 | 1.50 | 0.00 | 0.00 |
| Change | ||||
| Equilibrium |
To continue, we need to assume that we will finish with an unknown quantity (say x) of one of the products (say C), consequently, we have
A + B ⇄ C +D
| [A] | [B] | [C] | [D] | |
| Initial | 1.25 | 1.50 | 0.00 | 0.00 |
| Change | ||||
| Equilibrium | x |
Following the same reasoning used in ‘Example 2’, we can fill the table as:
A + B ⇄ C +D
| [A] | [B] | [C] | [D] | |
| Initial | 1.25 | 1.50 | 0.00 | 0.00 |
| Change | -x | -x | x | x |
| Equilibrium | 1.25 – x | 1.50 – x | x | x |
Replacing these values and the value of the equilibrium constant, we have:
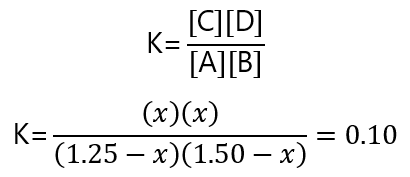
x2 = 0.10(1.25- x) (1.50 – x)
x2 = 0.10(1.875 – 1.25x – 1.50x +x2)
x2 = 0.10(1.875 – 2.75x +x2)
x2 = 0.1875 – 0.275x +0.10x2
0.90x2 + 0.275x – 0.1875 = 0
This is a quadratic equation with 2 solutions:
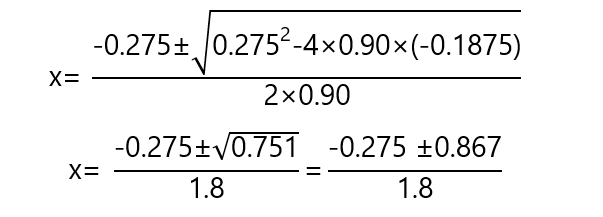
One of the solutions is negative, we can discard it as it has not physical meaning in the contest of the problem. The positive solution:
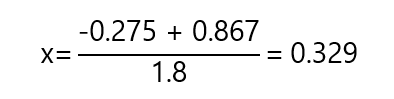
Therefore, the answers to the concentrations in equilibrium are:
[C] = [D] = 0.329 M
[A] = 1.25 – 0.329 = 0.921 M
[B] = 1.50 – 0.329 = 0.171 M
And we check that these values give the right constant by replacing them in the equation:
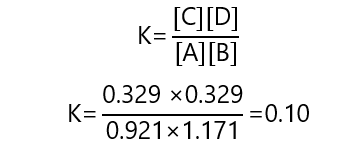
Exercises
Le Chatelier principle
1. The reaction between gaseous sulfur dioxide and oxygen to form sulfur trioxide is given by the reaction:
2SO2(g) + O2(g) ⇄ 2SO3(g)
What will be the effect of increasing the volume in the reaction?
Answer
We have 3 moles of gasses on the left and 2 mol of gasses on the right. An increase in volume will lead to a reduce in pressure. The system will try to compensate this reduction in pressure by increasing it and shifting to the left, where we have more moles of gasses.
2. The equilibrium between hydrogen and iodine to form hydrogen iodide is given by the reaction:
H2 + I2 ⇄ 2HI
What will be the effect of adding more hydrogen to the system?
Answer
The addition of H2 will shift the system to the right to reduce the presence of H2.
3. The reaction between nitrogen (N2) and oxygen (O2) to produce nitric oxide (NO) is:
N2 + O2 ⇄ 2NO
is an endothermic reaction. What will be the effect of reducing the temperature of the system?
Answer
As the reaction is endothermic, we can write:
Heat + N2 + O2 ⇄ 2NO
A reduction of temperature will shift the reaction to the left, as the system will try to generate more heat.
Equilibrium constants
4. Write the equilibrium constant to the following reactions:
a) N2O4 ⇄ 2NO2
b) 2NO2 ⇄ N2O4
c) H2 + Br2 ⇄ 2HBr
d) 2SO2 + O2 ⇄ 2SO3
Answer
a)
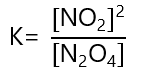
b)
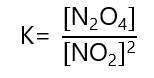
The K in b) is the reciprocal of K in a)
c)
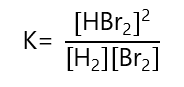
d)
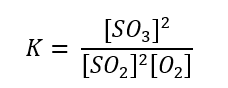
5. The reaction between gaseous sulfur dioxide and oxygen to form sulfur trioxide is given by the reaction:
2SO2(g) + O2(g) ⇄ 2SO3(g)
A mixture of SO2 and O2 was allowed to reach equilibrium and the following concentrations were found:
-
- SO2: 3.0×10-3 M
-
- O2: 3.7×10-3 M
-
- SO3: 4.0×10-2 M
What is the value of the equilibrium constant?
Answer
The equilibrium constant is:
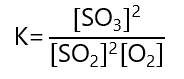
Replacing the values given:
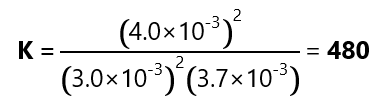
6. Hydrogen gas and iodine react to form hydrogen iodide via the reaction
H2+I2 ⇄ 2HI
A mixture of H2 and I2 was allowed to reach equilibrium. The equilibrium mixture contained
-
- HI: 1.37×10-2 M
-
- H2: 6.47×10-3 M
-
- I2: 5.94 x10-4 M
What is the equilibrium constant?
Answer
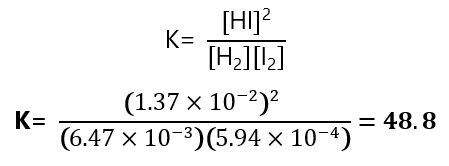
7. Nitrosyl chloride (NOCl) decomposes in nitric oxide (NO) and chlorine (Cl2) as per the following reaction:
2NOCl ⇄ 2NO + Cl2
NOCl was placed in a reactor to a concentration 0.75 M, heated and allowed to reach equilibrium. The contents of the reactor were then analysed and found that the concentration of Cl2 was 0.03M. What is the value of constant of equilibrium?
Answer
We start by identifying what are the initial components and those in equilibrium given by the wording of the problem
2NOCl ⇄ 2NO + Cl2
| [NOCl] | [NO] | [Cl2] | |
| Initial | 0.75 | 0 | 0 |
| Change | |||
| Equilibrium | 0.03 |
In the next step, we identify what are the changes of the different species:
Cl2: we started with 0 and in the equilibrium is 0.03, the change is therefore 0.03
NO: from the stoichiometry of the reaction, we know that for every mol of Cl2 produced, 2 mol of NO is produced, thus:
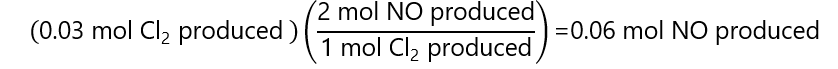
NOCl: from the stoichiometry of the reaction, we know that for every mol of Cl2 produced, 2 mol of NOCl is consumed, consequently:
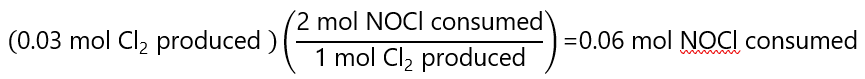
We can continue filling the table:
2NOCl ⇄ 2NO + Cl2
We can continue filling the table:
2NOCl ⇄ 2NO + Cl2
| [NOCl] | [NO] | [Cl2] | |
| Initial | 0.75 | 0 | 0 |
| Change | -0.06 | 0.06 | 0.03 |
| Equilibrium | 0.03 |
And complete the last row by adding the two previous rows:
2NOCl ⇄ 2NO + Cl2
| [NOCl] | [NO] | [Cl2] | |
| Initial | 0.75 | 0 | 0 |
| Change | -0.06 | 0.06 | 0.03 |
| Equilibrium | 0.69 | 0.06 | 0.03 |
And replace these values in the constant of the equilibrium:
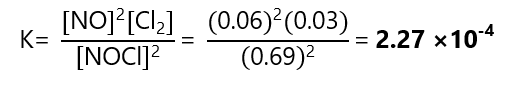
8. At high temperature, hydrogen (H2) reacts with carbon dioxide (CO2) to produce carbon monoxide (CO) and water (H2O) following the equation:
H2+CO2 ⇄ H2O + CO
If the equilibrium constant is K= 0.106 and the initial concentrations were 0.0150 M of H2 and 0.0150 M CO2, what are the concentration in equilibrium of all the species?
Answer
We are given the initial concentrations, but not the concentrations in equilibrium. I will call x the concentration of water in equilibrium, so, we can write:
H2+CO2 ⇄ H2O + CO
| [H2] | [CO2] | [H2O] | [CO] | |
| Initial | 0.0150 | 0.0150 | 0 | 0 |
| Change | ||||
| Equilibrium | x |
As all the coefficients are 1, filling the rest of the table is straightforward:
H2+CO2 ⇄ H2O + CO
| [H2] | [CO2] | [H2O] | [CO] | |
| Initial | 0.0150 | 0.0150 | 0 | 0 |
| Change | -x | -x | +x | +x |
| Equilibrium | 0.0150-x | 0.0150-x | x | x |
And the replacing these values in the constant of equilibrium:
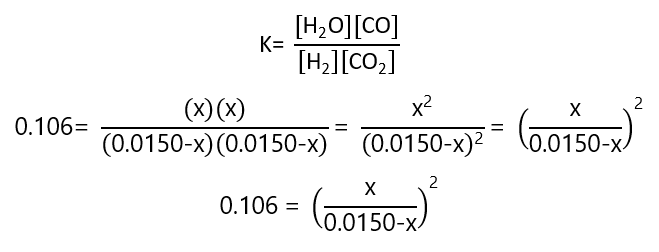
We can solve the quadratic equation developing the square and using the general equation for quadratic equations. However, as the equation appears, it is easy to take the square root in both sides of the equation, simplifying the operations (this is usually applicable when the initials concentrations are the same, as in Exercise 9, but not when they are different as we see in Exercise 9):
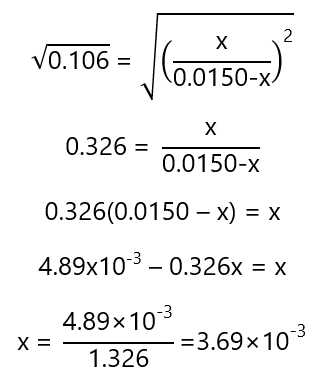
With the value of x, we can find the concentrations in equilibrium:
H2+CO2 ⇄ H2O + CO
| [H2] | [CO2] | [H2O] | [CO] | |
| Initial | 0.0150 | 0.0150 | 0 | 0 |
| Change | – 3.69×10-3 | – 3.69×10-3 | 3.69×10-3 | 3.69×10-3 |
| Equilibrium | 0.01131 | 0.01131 | 0.00369 | 0.00369 |
We can check that this is the right answer by inserting the values obtained in the expression of K and verify that match with the one given:
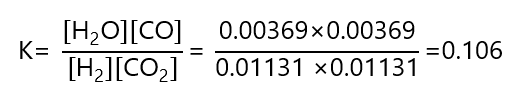
9. Repeat Exercise 8, but using initial concentration of 0.700 M CO2 and 0.800 M H2
Answer
Following the same steps than in Exercise 8, we can see that:
H2+CO2 ⇄ H2O + CO
| [H2] | [CO2] | [H2O] | [CO] | |
| Initial | 0.800 | 0.700 | 0 | 0 |
| Change | -x | -x | +x | +x |
| Equilibrium | 0.850-x | 0.700-x | x | x |
And the replacing these values in the constant of equilibrium:

Solving the quadratic equation
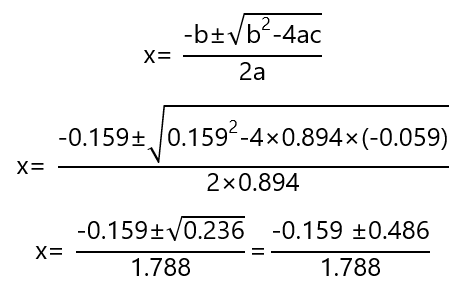
These gives 2 answers: one negative that has no meaning for the problem, the positive answer is
x = (-0.159 + 0.486)/1.788 = 0.183
With this result, we get:
H2+CO2 ⇄ H2O + CO
| [H2] | [CO2] | [H2O] | [CO] | |
| Initial | 0.800 | 0.700 | 0 | 0 |
| Change | – 0.183 | – 0.183 | 0.183 | 0.183 |
| Equilibrium | 0.617 | 0.517 | 0.183 | 0.183 |
We can check that this is the right answer by inserting the values obtained in the expression of K and verify that match with the one given:
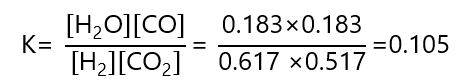
Reasonably close, accounting for rounding errors.
10. Hydrogen (H2) reacts with iodine (I2) to produce hydrogen iodide (HI) according to the following chemical equation:
H2+I2 ⇄ 2HI
If the K = 54 and the initial concentrations of H2 and I2 are 0.172 M. What are the equilibrium concentrations?
Answer
Using the same development of exercise 8, we can see that
H2+I2 ⇄ 2HI
| [H2] | [I2] | [HI] | |
| Initial | 0.172 | 0.172 | 0 |
| Change | |||
| Equilibrium | x |
From the stoichiometry, we see that for every mol of H2 or I2, we form 2 mol of HI, then
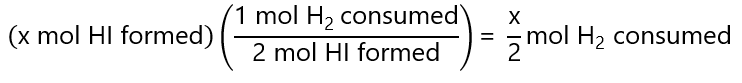
And the same for I2, hence:
H2+I2 ⇄ 2HI
| [H2] | [I2] | [HI] | |
| Initial | 0.172 | 0.172 | 0 |
| Change | –x/2 | –x/2 | +x |
| Equilibrium | 0.172 – x/2 | 0.172 – x/2 | x |
Inserting these values in K:
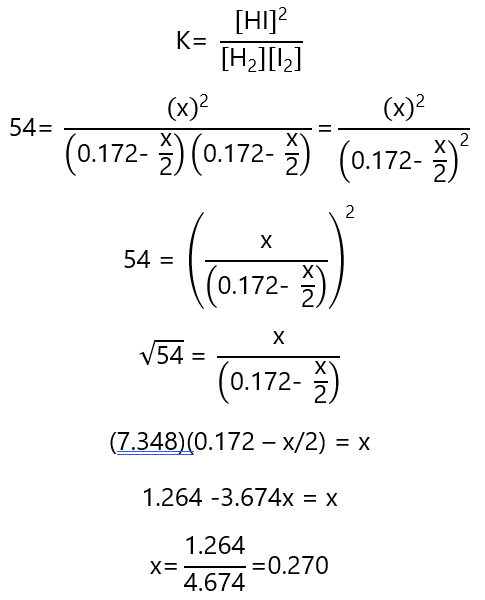
We can find the concentrations in equilibrium:
H2+I2 ⇄ 2HI
| [H2] | [I2] | [HI] | |
| Initial | 0.172 | 0.172 | 0 |
| Change | – 0.135 | – 0.135 | 0.270 |
| Equilibrium | 0.037 | 0.037 | 0.270 |
Again, we can check that this is the right answer by inserting the values obtained in the expression of K and verify that match with the one given:
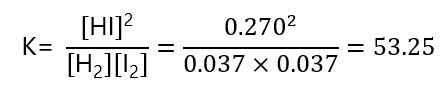
The value is not exactly 54 due to rounding errors, if we use 4 decimal places, and take [HI] = 0.2704 and [I2] = [H2] = 0.0368, we obtain K = 53.99
11. Repeat Exercise 10, but using concentrations of 0.200 M H2 and 0.300 M I2 are 0.172 M.
Answer
Following the reasoning of Exercise 10, we can find the following concentrations:
H2+I2 ⇄ 2HI
| [H2] | [I2] | [HI] | |
| Initial | 0.200 | 0.300 | 0 |
| Change | – x/2 | – x/2 | +x |
| Equilibrium | 0.200 – x/2 | 0.300 – x/2 | x |
Inserting these values in K:
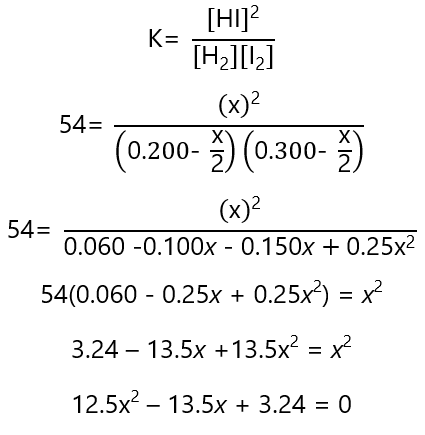
Solving the quadratic equation:
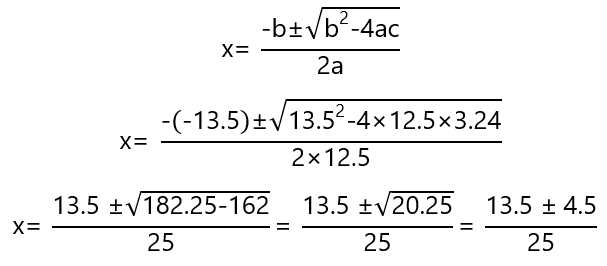
These equation gives 2 positive answers: 0.72 and 0.36. 0.72 will give negative values in the concentration at equilibrium of H2 (0.200 – 0.72/2 = – 0.16) and I2 (0.300 – 0.72/2 = – 0.06), therefore we discard it and use x = 0.36 and get:
H2+I2 ⇄ 2HI
| [H2] | [I2] | [HI] | |
| Initial | 0.200 | 0.300 | 0 |
| Change | -0.18 | -0.18 | 0.360 |
| Equilibrium | 0.020 | 0.120 | 0.360 |
we can check that this is the right answer by inserting the values obtained in the expression of K and verify that match with the one given: