On this page, I’m talking about how to measure the concentration of solutions, i.e. how much sample we have in a hetererogeneous system.
The outline for this page is:
1. Solutions
2. Molarity (M)
a) Equivalent and equivalent mass
b) Normality
4. Molality (m)
6. Concentration expressed in physical units
a) Mass of solute by volume of solution
c) Parts per … million, billion, …
7. Dilutions
8. Exercises
a) Molarity
b) Normality
c) Molality
e) Concentrations expressed in physical units
f) Dilutions
9. Comments
1. Solutions
When you think of a solution, you might think in things like sugar or salt dissolved in water. Yes, you are right, this is a solution. We can define a solution as a homogeneous mixture of two components:
- The solute that is the substance that has been dissolved and is in minor proportion (like the sugar).
- The solvent is the substance in which the solute dissolved and is the major component of the mixture (like the water).
Most of the common solvents are liquid, being water the most common one. We will work with liquid solvents here, however, you should be aware that solutions can be also gasses (for example, the air is a solution of where the solvent is nitrogen, ~80%, and the solute is the oxygen, ~ 20%) or solids (like the bronze, where the solvent is copper, typically ~88%, and tin, ~12%). Solute can be solid, liquid or gas, and we might have more than one solute.
In chemistry, we usually work with solutions, and we need to know how much of a given substance we have in solution. This is achieved by knowing the concentration. There are different ways of measure the concentrations, no, it is not that we like to complicate things, the other way round, given a particular task, it is easier to work if a concentration is given in certain units. We can refer to concertation using physical terms (kg/L, % by volume, …) or chemical terms. The most common concentration units using chemical terms are shown in table 1.
| Concentration units | Expression | Notes |
|---|---|---|
| Molarity (M) | Mol of solute/Litre of solution | Useful in volumetric analysis: the amount of solute is related to the measured volume of solution. It is temperature dependent (as volume depends on temperature) |
| Normality (N) | Equivalent of solute/Litre of solution | Useful in volumetric analysis: very convenient for comparing the relative volumes for solutions that react which other.Reaction dependent: for a given solution, normality can be different depending the reaction under study. Temperature dependent (as volume depends on temperature) |
| Molality (m) | Mol solute / kg solvent | Useful for analysis of physical properties (freezing and boiling point, vapour and osmotic pressure, …) over a wide range of temperatures. It is independent of the temperature. For dilute aquous solutions (< 0.1 M) molarity and molality are numerically close. |
| Mole fraction (XA) | Moles of component A / Total moles in solution | Useful in study of collative properties (properties of the solution vary with the concentration of solute particles, often regardless of chemical composition) such as freezing point, boiling point, vapor pressure, and osmotic pressure. |
| Physical units | Various expressions: mass / volume % composition Parts per … million, billion, … | Physical units provide a common language across different disciplines. Generally more practical and intuitive than concentrations based in chemical units. |
Before we start, I use the factor label method (also called unit factor method or dimensional analysis), if you are not familiar with it, you can see it by clicking here.
2. Molarity (M)
Molarity (M) is the number of moles solute in one litre of solution:
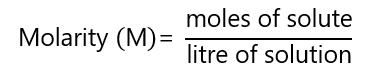
The unit is ‘molar’ represented by M. If you want to review concepts of mol, atomic mass, etc., click here.
Example 2.1
What is the molarity of a solution produced dissolving 3.0 moles of solute to 1.5 L of solution?
Answer
From the definition:
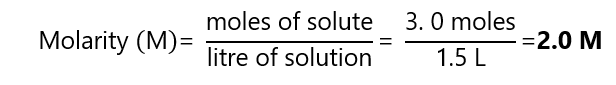
Example 2.2.
How many moles of solute do we have in 2.5 L of a 2.0 M solution?
Answer
As M is mol/litre of solution, we can see that:
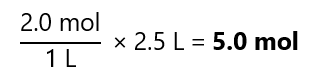
Example 2.3
What is the volume of a 2.0 M solution containing 5.0 moles of solute?
Answer
From the definition of M and the values given, we can write the following equation:
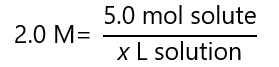
And solve the value of x as
x = 5.0 / 2.0 = 2.5 L
Example 2.4
What is the molarity of a 0.5 L solution containing 149.2 g of potassium chloride (KCl)? Molecular mass KCl: 74.6 g/mol
Answer
Dividing the mass of KCl by its molecular mass, we obtain the number of mol:
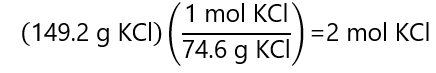
And dividing this number by the volume (in L), we obtain:

3. Normality (N)
Normality is the only common concentration used in chemistry that depend on the chemical reaction being studied. For this reason, you will find that normality is mainly used in acid-base and redox reactions, where it simplifies the calculation. In other cases, concentrations are usually defined in other units that are more relevant.
Normality (N) is defined as the number of equivalents of solute per litre of solution. Its unit is called normal.
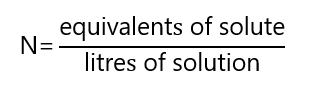
Before working with normality, we need to define equivalent.
a) Equivalent and equivalent mass
Traditionally, equivalent mass is known as equivalent weight, this term is still widely use in chemistry. Equivalent mass is defined as the mass in grams of 1 equivalent of substance:
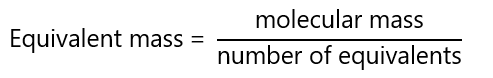
The definition of equivalent depends on the type of reaction under study: acid-base reactions or redox reactions.
In acid base reactions
For an acid-base reaction, one equivalent is the quantity of a substance that will react with or yield 1 mol of hydrogen ions (H+) or hydroxide ions (OH–).
The equivalent will depend on the reaction under study. The simplest cases are for acids or bases that reacts or produce with only 1 hydrogen ion or hydroxide ion. For example, hydrochloric acid (HCl) when involved in an acid base reaction production 1 mol of hydrogen ions (H+) per mol of hydrochloric acid (HCl):
HCl → Cl– + H+
Therefore, the equivalent of the HCl is:
1 equivalent = 1 mol HCl.
And the equivalent weight is the mass of 1 mol of HCl (taking its molecular mass as 36.5 g/mol):
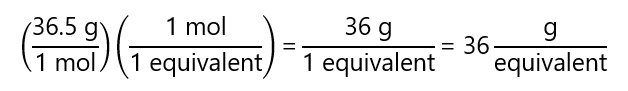
In the case of the strong acid or bases (i.e. that are completely or nearly 100% ionized in their aqueous solutions), the equivalent is the number of H+ or OH– that they have. For example, the barium hydroxide (Ba(OH)2), that is a strong base, dissociate providing 2 OH–:
Ba(OH)2 → Ba2+ + 2OH–
Therefore, the equivalent weight is:
2 equivalents = 1 mol Ba(OH)2
And the equivalent mass (taking its molecular mass as 171.3 g/mol):
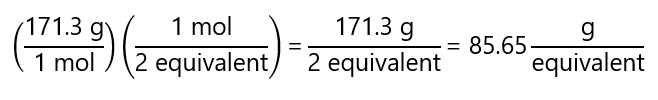
The problem is more complex when we have acids or bases that contain two or more H+ or OH– with different tendencies to dissociate. For example, the phosphoric acid (H3PO4), with a molecular mass = 98 g/mol, has 3 protons. The protons can be dissociated separately under the right conditions, and we have 3 possible cases:
a) H3PO4 → H2PO3– + H+
In this case, 1 mol of H3PO4 yield 1 mol of H+, therefore:
valent = 1 mol H3PO4.
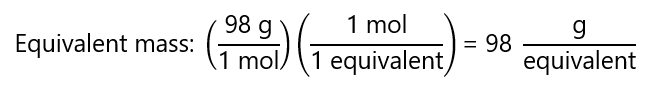
b) H3PO4 → HPO32- + 2H+
In this case, 1 mol of H3PO4 yield 2 mol of H+, therefore:
2 equivalents = 1 mol H3PO4.
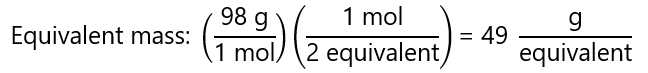
c) H3PO4 → PO33- + 3H+
In this case, 1 mol of H3PO4 yield 2 mol of H+, therefore:
3 equivalents = 1 mol H3PO4.
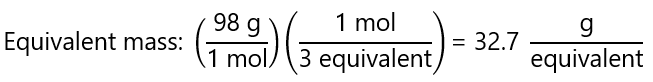
Example 3.1
Calculate the equivalents and equivalent masses in 98 g of sulfuric acid (H2SO4) in each of the following reactions:
Reaction a: H2SO4 + NaOH → NaHSO4 + H2O
Reaction b: H2SO4 + 2NaOH → Na2SO4 + 2H2O
Molecular mass H2SO4 = 98 g/mol.
Answer
Since we have 98 g of H2SO4, i.e. 1 mol, we can see that:
- In the reaction a):
- 1 mol of H2SO4 reacts with 1 mol of OH–, we can consider that 1 equivalent of H2SO4 = 1 mol of H2SO4.
- The equivalent mass is therefore 98 g / 1 equivalent = 98 g/equivalent.
- In the reaction b),
- 1 mol of H2SO4 reacts with 2 mol of OH–, we can consider that 2 equivalents of H2SO4 = 1 mol of H2SO4.
- The equivalent mass is therefore 98 g / 2 equivalent = 49 g/equivalent.
Example 3.2
Calculate the number of equivalents of 2 mol of sulfuric acid (H2SO4) in the following reaction:
H2SO4 + 2NaOH → Na2SO4 + 2H2O
Answer
As we have seen in the previous example, for this reaction we have 2 equivalents per mol, therefore, for 2 mol we have:
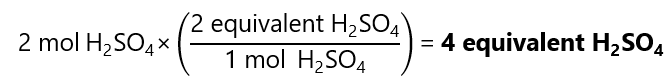
In redox reactions
I have talked about redox equations on another page, if you need a refresher, click here.
In a redox reaction, an equivalent is the quantity of a substance that will react with or yield 1 rnol of electrons.
To check the number of electrons transferred, we can either
- check the electrons that appear in the half equations or
- check the oxidation state the specie and deduct from there the number of electrons involved.
For example, given the reaction:
MnO4– + 5Fe2+ + 8H+ → Mn2+ + 5Fe3+ + 4H2O
What is the equivalent of MnO4–? (This reaction is the 3rd exercise on ‘How to balance redox equations’). What is the equivalent mass, considering that it is provided as KMnO4 (potassium permanganate) with a molecular mass = 158 g/mol?
If we check the half equation:
MnO4– + 8H+ + 5e–→ Mn2+ + 4H2O
We can see that 1 mol of MnO4– reacts with 5 mol of e–, therefore, in this reaction, 5 equivalents = 1 mol of MnO4–.
An alternative method is to investigate the oxidation state of the manganese in the products and in the reactants and find the number of electrons involved on the change:
- The oxidation state of the manganese in MnO4– is +7:
- The oxidation state of the manganese ion Mn2+ is, obviously, +2
Therefore, the manganese change from +7 to +2, the difference is due the 5 electrons:
Mn(+7) + 5e–→ Mn(+2)
and we reach the same conclusion than before: 5 equivalents = 1 mol of MnO4–. The equivalent mass is:
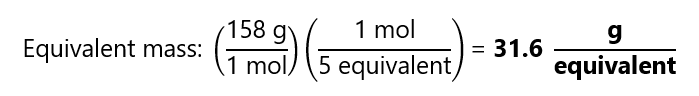
Example 3.3.
How many equivalents and equivalent mass do we have in 1 mol of ion sulfate (SO42-) in the following reaction?
SO42– + 4Zn + 10H+ → H2S + 4Zn2+ + 4H2O
Formula mass SO42-: 96 g/mol
Note, this equation is the example 16 from ‘How to balance redox equations’.
Answer
In the equation, we have the sulfur change from oxidation state +6 in the sulfate (SO42-) to oxidation state -2 in the hydrogen sulfide (H2S), requiring 8 electrons for it:
S(+6) + 8e– →S(-2)
Alternatively, we can check the 8 electrons required by obtaining the half equation for this reaction:
SO42- + 10H+ + 8e–→ H2S + 4H2O
In both cases, we obtain that we require 8 mol of electron per mol of ion sulfate, therefore we have 8 equivalents = 1 mol of SO42-.
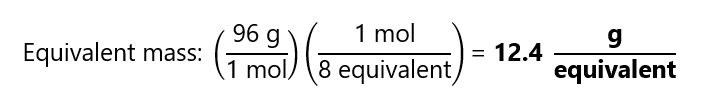
Example 3.4
How many equivalents are there and what is the equivalent mass in 1 mol of zinc from the equation seen in the previous example:
SO42– + 4Zn + 10H+ → H2S + 4Zn2+ + 4H2O
Atomic mass Zn: 65.4 g/mol
Answer
From the stoichiometry of the reaction, we can see that the oxidation of the Zn is:
Zn → Zn2+ + 2e–
Therefore, 2 equivalents = 1 mol Zn.
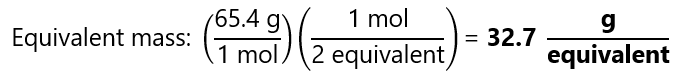
b) Normality
Normality (N) is defined as the number of equivalents of solute per litre of solution. Its unit is called normal.
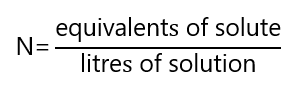
It is also common to express the normality as milliequivalents per millilitre (meq/mL), it is the same than eq/L.
Equivalents are very useful in dealing with titrations. Titrations are used to find the concentration of one specie via chemical reactions with another specie of known concentration, and they will be explained in other webpages in the near future. In titrations, as 1 equivalent of one substance reacts with 1 equivalent of another substance in the reaction, we have:
Equivalent of substance 1 = Equivalent of substance 2
N1V1 = N2V2
Where: Ni is the normality of substance i
Vi is the volume of the substance i
The V1 and V2 are typically expressed in L, but it can be any other unit of volume as long as V1 and V2 are expressed in the same units. See ‘Example 3.10’.
Sometimes we need to convert molarity to normality and vice versa, they are related by the expression:
N = M*n
Where: N = Normality
M = Molarity
n = number of equivalents.
We use this expression in ‘Example 3.11’ and ‘Example 3.12’.
Example 3.5
What is the normality of a solution that contains 5 equivalents in 2.5 L of solution?
Answer:
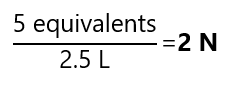
Example 3.6
What is the normality of a 1.5 M sulfuric acid (H2SO4) in each of the following reactions:
Reaction a: H2SO4 + NaOH → NaHSO4 + H2O
Reaction b: H2SO4 + 2NaOH → Na2SO4 + 2H2O
Answer
We found in the ‘Example 3.1’ (acid base reactions above), that there are 1 equivalent per mol in reaction a and 2 equivalents per mol in reaction b. Using these factors, we can see that:
- Reaction a:
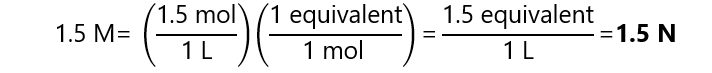
- Reaction b:
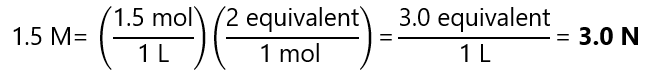
Example 3.7
What is the molarity of 2 N of sulfuric acid (H2SO4) in the following reactions:
Reaction a: H2SO4 + NaOH → NaHSO4 + H2O
Reaction b: H2SO4 + 2NaOH → Na2SO4 + 2H2O
Reaction c: H2SO4 + 8H+ + 8e–→ H2S + 4H2O
Equivalents can be found in ‘Example 3.6’ and in ‘Example 3.3’.
Answer
Reaction a:
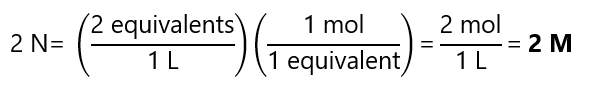
Reaction b:
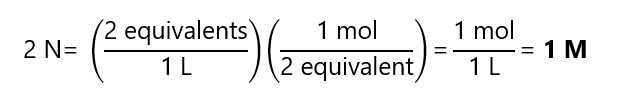
Reaction c:
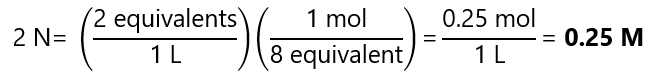
Example 3.8
How many equivalents are present in 2 L of a 3 N solution?
Answer
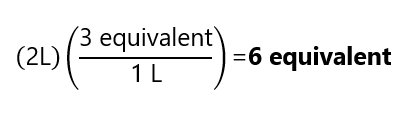
Example 3.9
What is the final concentration of HCl if 2.0 L of 2.0 N HCl and 1.5 L of 3.0 N are mixed and diluted to 5 L?
Answer
We calculate the number of equivalents provided by of each solution and divided its addition by the final volume:
(2.0 L) * (2.0 N) = 4.0 equivalents
(1.5 L) * (3.0 N) = 4.5 equivalents
Total: 4.0 + 4.5 = 9.5 equivalents
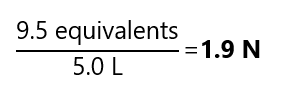
Example 3.10
What is the volume of 3.0 N sodium hydroxide (NaOH) required to neutralize 50.0 mL of 2.0 N sulfuric acid (H2SO4)?
Answer
N1V1 = N2V2
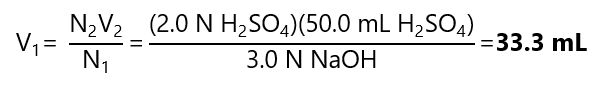
Example 3.11
Calculate the normality of:
a) 1M sulfuric acid (H2SO4)
b) 1 M sodium hydroxide (NaOH)
Answer
a) As H2SO4 provides 2 H+, its equivalent is 2, therefore:
N = M*n
N = 1*2
N = 2
So, 1M H2SO4 = 2N H2SO4.
b) As NaOH provides 1 OH–, its equivalent is 1, therefore:
N = M*n
N = 1*1
N = 1
So, 1M NaOH = 1N NaOH.
Example 3.12
Calculate the molarity of:
a) 1N hydrochloric acid (HCl)
b) 1 N barium (Ba(OH)2)
Answer
a) As HCl provides 1 H+, its equivalent is 1, therefore:
N = M*n
1 = M*1
M = 1/1 = 1
So, 1N HCl = 1M HCl.
b) As Ba(OH)2 provides 2 OH–, its equivalent is 2, therefore:
N = M*n
1 = M*2
M = 1/2 = 0.5
So, 1N Ba(OH)2 = 0.5 M Ba(OH)2.
4. Molality (m)
Molality (m) is the number of moles solute in one kilogram of solvent:
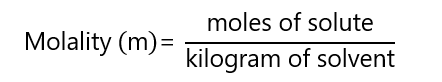
The units of molarity and molality are confusing at the beginning, as they look very similar. Be careful with the differences between molality and molarity:
- Molality is defined in terms of kilograms, not litres.
- Molality is defined in terms of solvent, not solution.
- The symbol for molality is a lowercase m, not capital M.
Example 4.1
Calculate the molality obtaining by adding 0.3 mol of solute to 250 g of water.
Answer
As 250 g of water is 0.25 kg, from the definition of molality, we have:
m = 0.3 mol solute / 0.25 kg solvent = 1.2 m
Example 4.2
What mass of H2O is required to make a 1.50 m solution with 0.75 mol NaCl?
Answer
From the definition of m, we can write the following equation:
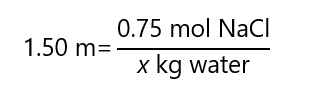
And solve the equation:
x = 0.75 / 1.50 = 0.5 kg of water
Example 4.3
What is the mass of a 1.25 m aqueous solution that contains 149.2 g of potassium chloride (KCl)? Molecular mass KCl: 74.6 g/mol
Answer
We are being asked with the mass of the solution, i.e. the mass of the solvent and the solute combined. We know the mass of the solute, we need to find the mass of the solvent. With the molecular mass and the mass, we know that:

From the molality, we find that:
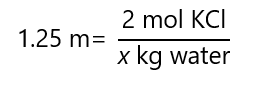
x = 2/1.25 = 1.6 kg water
Adding the mass of water (1.6 kg = 1,600 g) with the mass of the KCl (149.2 g) we obtain:
1,600 g + 149.2 g = 1,649.2 g
5. Mole Fraction (XA)
The mole fraction of a substance A in a solution (usually expressed as XA) is the ratio of the number of moles of that substance to the total number or moles in the solution. For example, if we have a solution containing x mol of A, y moles of B and z moles of C, the molar fraction of A is:
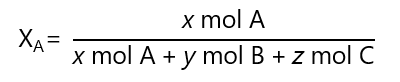
Molar fraction is dimensionless (it has no units). The addition of all molar fractions in a solution should be 1, for example, in the solution of 3 components A, B and C:
XA + XB + Xc = 1
Example 5.1
What is the mole fraction of 18 g of glucose (C₆H₁₂O₆, molar mass: 180 g/mol) and 36 g of water (H2O, molar mass: 18 g/mol)
Answer
We start by calculating the number of mol of each component:
Glucose:
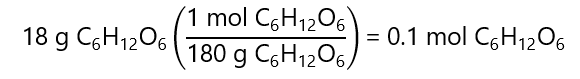
Water:
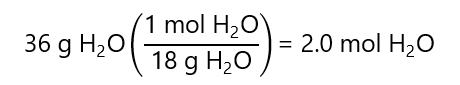
Mole fraction glucose:
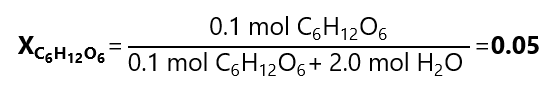
6. Concentration expressed in physical units
a) Mass of solute by volume of solution
As the definition indicates, you express the mass of the solute by volume of solution, for example 50 g of NaCl per litre [of solution] (the end ‘of solution’ is usually omitted, as it is understood for the contest). The units are not standardized, and you will find that can be mg/mL, g/mL, kg/L, …
Example 6.1
5 g of KCl is dissolved and diluted to 100 mL in water. Calculate the concentration in g/mL, mg/mL, mg/cm3 and kg/m3.
Answer
Expression in g/mL is straight forwards, as it only requires making a division:
5 g / 100 mL = 0.05 g/mL
In the rest, we need to transfer the units. I will be using the factor label method. If you have or prefer another method, feel free to use it and compare the results, we should have be the same results (accounting for any rounding errors).
Expression in mg/mL:
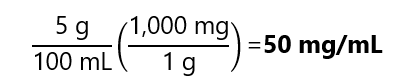
Expression in mg/cm3:
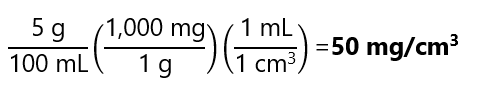
Expression in kg/m3:
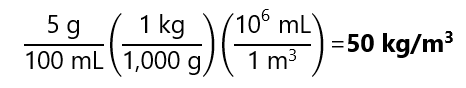
As we can see from these results, mg/mL, mg/cm3 and kg/m3 are equivalent units.
Example 6.2
How many grams of sodium carbonate (Na2CO3) are required to prepare 50 mL of a solution of Na2CO3 with concentration 20 g/L
Answer
First, we transform the concentration for g/L to g/mL:
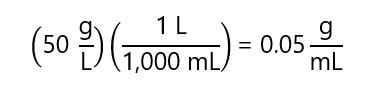
With this answer, we calculate how many g will need to prepare 50 mL:

b) By percentage composition
It is referred to the relation of number of units of solute per 100 units of solution:
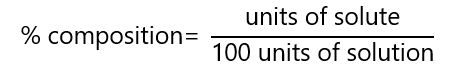
The most common units are mass and volume:
- Weight by weight percentage, mass percentage or %w/w refers to mass units of solute per 100 mass units of solution. For example: a solution 20% weight by weight of NaCl means that there 20 g of NaCl for every 100 g of solution (if the units are not indicated, you can use whatever units are more convenient, as long as they are the same, i.e. g/g, kg/kg, etc.).
- Volume by volume percentage, volume percentage or %V/V refers to the volume unit of solute per 100 volume units of solution. For example: a solution 30% volume by volume of ethanol indicates that there are 30 mL of ethanol for every 100 mL solution (if the units are not indicated, you can use whatever units are more convenient, as long as they are the same, i.e. mL/mL, L/L, etc.).
- Weight by volume percentage or %w/v indicates the number of mass unit of solute per 100 volume units of solution. For example, a 15% mg/mL indicates that there are 15 g of solute per 100 mL of solution.
Sometimes we are given the units of solvent and solution and we are asked to calculate the percentage. For example, what is the percentage in g/ml of 0.5 g of magnesium chloride (MgCl2) dissolved to 25 mL with water. The formula to calculate percentage solution is:
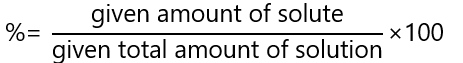
Therefore, in our case:
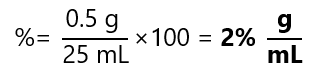
Example 6.3
How many grams of calcium bromide (CaBr2) we need to dissolve in water to prepare 30 grams of a 20% w/w solution?
Answer
20% w/w means 20 g of CaBr2 per 100 g of solution, if we need 30 g of solution, we need:
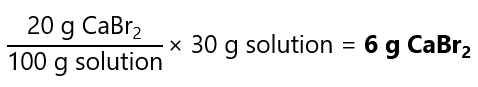
Example 6.4
How many mL of methanol we need to dilute with water to obtain 2 L of 20% V/V of ethanol in water?
Answer
As we are asked the number of mL of methanol, I will use the %V/V in mL and use 2,000 mL of solution instead of 2 L (it makes the calculation easier) 20% V/V means 20 mL of ethanol for every 100 mL of solution:

As we need 1 L (or 1,000 mL):

If you prefer to use 2 L of solution instead of 2,000 mL, using the factor label method the answer is:
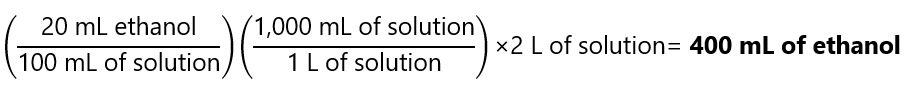
Example 6.5
How many mg of aluminium chloride (AlCl3) we need to dissolve in water to 25 mL to obtain a concentration of 1% g/ml?
Answer
As 1% g/mL means 1 g for 100 mL of solution, we obtain that to prepare 25 mL we need:
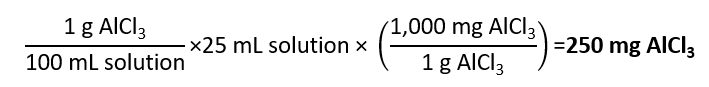
c) Parts per … million, billion, …
These measurements are not part of the International System on Units (SI), however, they are quite used and very common when dealing with very diluted solutions, like contaminants in the water. When working with water as solvent, it is considered that 1 kg is the equivalent to 1 L of solution (the density of the water is 1.00 g/mL (or 1.00 kg/L)). For example, as the mercury is highly poison, the maximum acceptable level of mercury in water for human consumption is 2 mg/L (or 2 x 10-6 g/L), yes, very small quantity. The two most common ones are:
- Part per million (ppm): is 1 part for every 1,000,000 (106) parts, for example: 1 mg/kg (also 1 mg/L for aqueous solutions)
- Part per billion (ppm): is 1 part for every 1,000,000,000 (109) parts, for example 1microg/kg. (Note that this is the English billion, that is equivalent to the European 1,000 million). So the acceptable levels of mercury in drinking water that we mentioned above is 2 ppb.
Example 6.6
Sea water contains 0.02 ppm of dissolved iron. What volume (in litres) of this sea water would contain 1.00 g of iron?
Answer
As 0.02 ppm means 0.02 mg gold/L of solution (I use L, as the question ask for L of water):
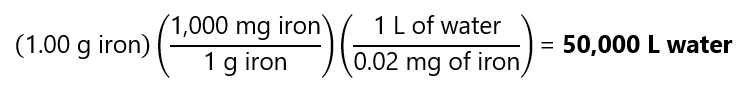
Example 6.7
Arsenic (As) is found in water in concentration of 3.2 x10-7 M. What is it concentration in ppb? Atomic mass of As: 75 g/mol
Answer
We express the concentration of As in g/L and we change to microg/L:
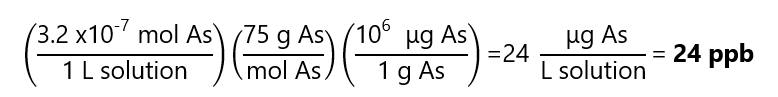
Example 6.8
Taking the density of air is 0.00012 gram/mL, what volume of air contain one gram of sulfur dioxide (SO2), if the sulfur dioxide concentration is 2 ppm? SO2 is a pollutant that can cause acid rains. Molecular mass SO2: 64.1 g/mol.
Answer
This is a case of a solution of gases, and we cannot use the approach that 1 L of solution is 1 kg of solution (as the density is not 1 g/mL). The concentration in ppm refers to 1 part for every 1,000,000 (106) parts, I will take the concentration of 2 ppm as 2 mg of SO2 /kg of air. We start by calculating the mass of air that contains 1 g (= 1,000 mg) of SO2:

Now with the density, we can calculate its volume:
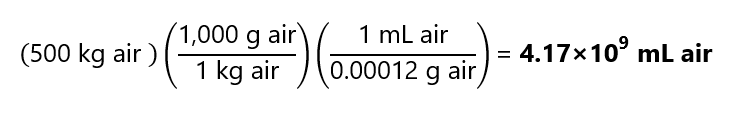
Example 6.9
If the concentration of aluminium (Al) in sea water is 2 ppm, what is its concentration in % w/w?
Answer
This is a simple conversion of units:

7. Dilutions
Dilution is the process of decreasing the concentration of a solute in a solution, typically by adding more solvent.
When the concentration is expressed as a fixed volume (like normality, molarity and % v/v and % w/v) we can express the concentration amount of solute as:
Amount of solute = volume * concentration.
If the dilution is performed by adding more solvent to the solution, the amount of solute does not change, but the concentration will decrease and the volume increase. Mathematically this can be expressed as:
CiVi = CfVf
Where: Ci: Initial concentration
Vi: Initial volume
Cf: Final concentration
Vf: Final volume
Ci and Cf have to be expressed in the same units. The same apply for Vi and Vf.
When the concentrations are not expressed in fixed volumes, we need to use the density to be able to apply this equation, see Example 7.3.
Sometimes dilutions are prepared by mixing solution of different concentrations. In these cases, the final amount of solute is the addition of the the amount provided by each solution:
Final amount of solute = solute from solution 1 + solute from solution 2 + …
Final amount can be equivalents when working with normality, moles when working with molarity, etc. See Example 7.4. In these exercises, sometimes we need to consider that the volumes are additive and that there is no volume contraction (this is not entirely true, as there is always some contraction).
Example 7.1.
To how many mL do we need to dilute 20.0 mL of a 0.5 M solution to obtain a 0.2 M solution?
Answer
Using
CiVi = CfVf
0.5 M x 20.0 mL = 0.2 M x Vf
Vf = (0.5 x 20.0) / 0.2 = 50.0 mL
This means that we need to add solvent to the initial 20.0 mL until we reach 50.0 mL, NOT that we need to add 50.0 mL of solvent.
Example 7.2
How many mL of a 1N solution do we need to prepare 100 mL of a 0.2 N solution?
Answer
As this a dilution (no chemical reactions), we can use:
CiVi = CfVf
1 N * Vi = 0.2 N * 100 mL
Vi = (0.2 * 100) / 1 = 20 mL
Example 7.3
How much sulfuric acid (H2SO4) of concentration 98% w/w and density 1.84 g/mL needs to be diluted with water to prepare 100.0 mL of 20% w/w H2SO4 with a density of 1.14 g/mL?
Answer
As the concentrations are not related to volume, we need to express these in terms of the volume using the density:
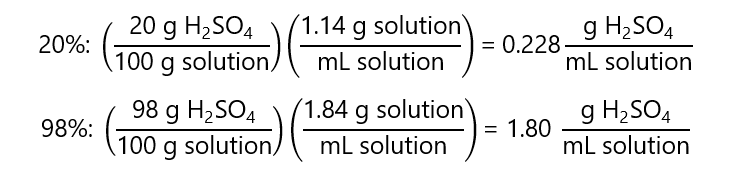
Now we can proceed with the formula:
CiVi = CfVf
0.228 g/mL * 100 mL = 1.80 g/mL * Vf
Vf = (0.228 * 100) / 1.80 = 12.7 mL
Example 7.4
What volumes of 0.5 N hydrochloric acid (HCl) and 0.1 N HCl must be mixed to obtain 4 L of 0.2 N HCl? Consider that there is no volume contraction.
Answer
The final amount of solute, measured in number of equivalents, is the addition of the number of equivalents from the 0.5 N HCl and 0.1 N HCl:
Number of equivalents 0.2 N = number of equivalents 0.5 N + number of equivalents 0.1 N
The final volume is 2 L, and as we are considering that there is volume contraction, let’s call v the volume (in L) of 0.5 N HCl and 2 – v the volume (in L) of the 0.1 N HCl. Then we can write:
0.2 N * 2L = 0.5 N * v + 0.1 N * (2 – v)
0.4 = 0.5 v + 0.1 * 2 – 0.1v
0.2 = 0.4v
V = 0.2/0.4 = 0.5 L
Therefore, we need 0.5 L of 0.5 N HCl and 1.5 L of 0.1 N HCl.
8. Exercises
a) Molarity
A.1. What is the molarity of a solution prepared by dissolving 234 g of sodium chloride (NaCl) in enough water to make 500.0 mL of solution? Molecular mass NaCl: 58.5 g/mol
Answer
The number of mol of NaCl is:
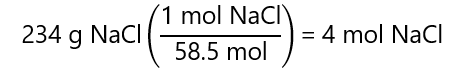
As 500.0 mL is 0.500 L:
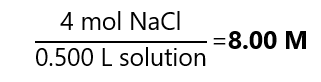
A.2. What is the final concentration of mixing 1 L of a 3M sodium chloride (NaCl) solution with 2 L of a 1.5 M sodium chloride (NaCl) solution and enough water to make 5 L?
Answer
The final number of mol NaCl is:
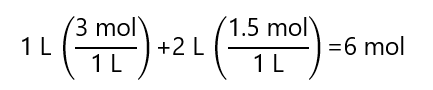
As the final volume is 5 L, the concentration is:
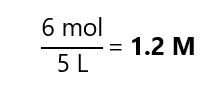
A.3. Calculate the molarity of the each of the following solutions:
a) 3 mol of solute on 1.5 L of solution
b) 2 mol of solute in 400 mL of solution
c) 0.4 mol of solute in 0.5 L of solution
Answer
a)
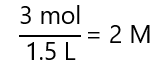
b)
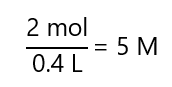
c)
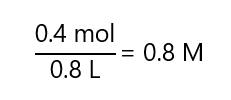
A.4. Calculate the number of moles of solute in each of the following solutions:
a) 2 L of 1.5 M solution.
b) 2 L of 0.75 M solution.
c) 250 mL of 1.5 M solution.
a) 75 mL of 3 M solution.
Answer
a)
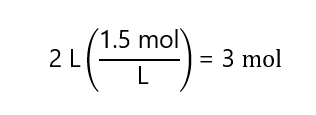
b)
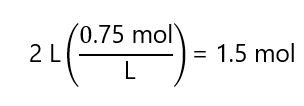
c)
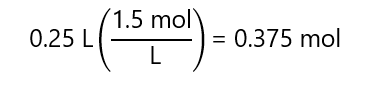
d)
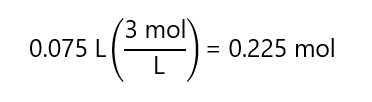
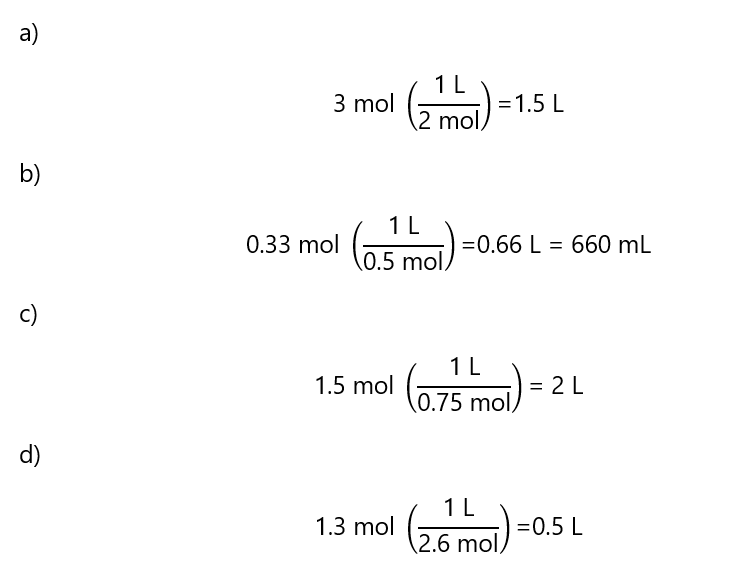
A.5. Calculate the volume required to prepare the following solutions:
a) 2 M solution containing 3 mol of solute
b) 0.5 M containing 0.33 mol of solute
c) 0.75 M containing 1.5 mol solute
d) 2.6 M containing 1.3 mol solute
Answer
A.6. What is the molarity of a solution obtained by dissolving 25.0 g of sodium chloride (NaCl) in water and adding water to make 500.0 mL of solution? Atomic mass NaCl: 58.44 g/mol
Answer
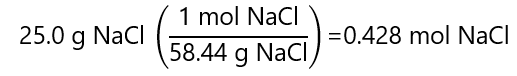
A.7. What volume of 2.5 M contains 100.0 g of sodium chloride (NaCl). Atomic mass NaCl: 58.44 g/mol
Answer
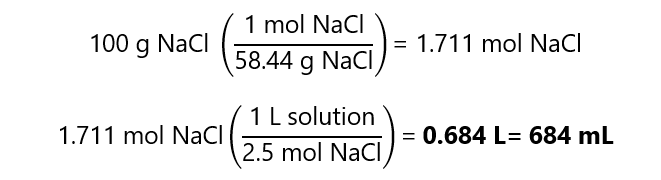
A.8. How many grams of sodium chloride (NaCl) we have in 500 mL of a 1.5 M NaCl solution? Atomic mass NaCl: 58.44 g/mol
Answer
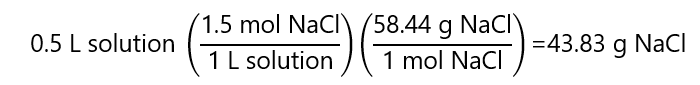
A.9. a) How many grams of lead (II) nitrate ((Pb(NO3)2) are required to prepare 1 L of 2 M Pb(NO3)2? b) What is the molar concentration of each ion? c) How many mL of the 2M solution contains 600 mg of Pb2+? Molar mass Pb(NO3)2 331.2 g/mol, Pb: 207 g/mol.
Answer
a)
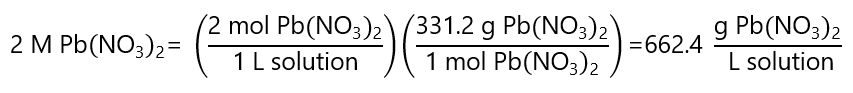
As we need 1 L of solution, we need 662.4 g of Pb(NO3)2.
b) From the formula, we can deduct that 1 mol of Pb(NO3)2 produce 1 mol Pb2+ and 2 mol of NO3–
Pb(NO3)2 → Pb2+ + 2NO3–
As we have 2 mol/L of Pb(NO3)2, we will have 2 mol/L (2M) Pb2+and 4 mol/L (4 M) NO3–.
c) As the concentration is 2 M Pb2+ and 600 mg Pb2+ = 0.6 Pb2+:
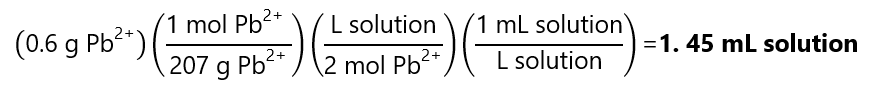
A.10. What is the molar concentration of a solution containing 174 g of acetone (C3H6O) in a 500 mL solution?. Molecular mass C3H6O: 58 g/mol
Answer
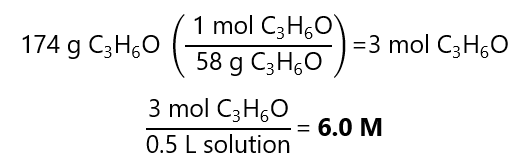
A.11. How much ammonium sulfate ((NH4)2SO4) is required to prepare 250 mL of a 0.5 M solution. Molecular mass (NH4)2SO4: 132 g/mol.
Answer

b) Normality
B.1. What volume of 2.0 N sulfuric acid (H2SO4) is completely neutralized by 40.0 mL of
a)20 N sodium hydroxide, NaOH
b) 20 M sodium hydroxide, NaOH
c) 20 N barium hydroxide, Ba(OH)2
d)20 M barium hydroxide, Ba(OH)2
Answer
a) As the reactions occur equivalent to equivalent, we can write:
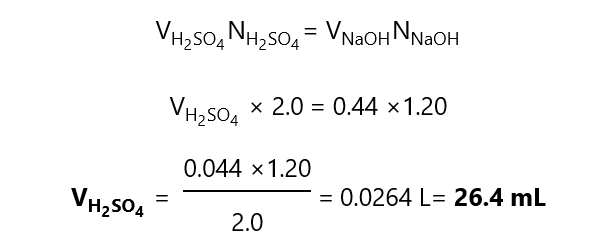
b) Since NaOH provides 1 OH–, its equivalent is 1 and the normality of the NaOH is the same than the molarity, therefore, the answer is the same than in a), i.e. 4 mL H2SO4.
c) We can refer to the same calculation that in a) As the reactions occur equivalent to equivalent, we can write:
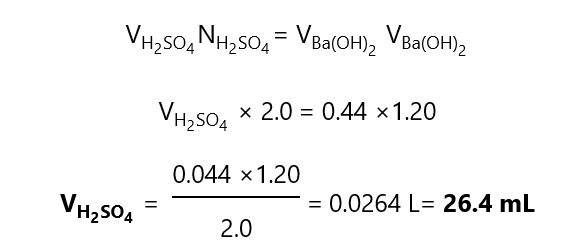
d) As the Ba(OH)2 provides 2 OH–:
N = M*n
N = 1.20 * 2
N = 2.40
And following the steps from a):
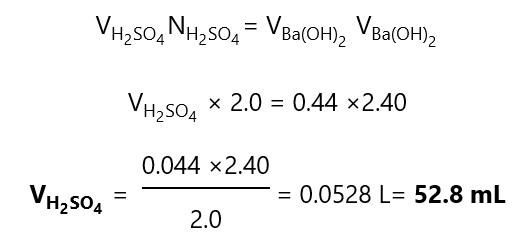
B.2. What mass of solute is required to prepare 1 L of 1 N solution of:
a) Potassium hydroxide (KOH). Molecular mass KOH: 56.1 g/mol
b) Iodine (I2), as oxidizing agent. Molecular mass I2: 253.8 g/mol
c) Phosphoric acid (H3PO4), replacing all 3 H+. Molecular mass: 98 g/mol.
Answer
a) As the KOH provides 1 OH–, 1 equivalent = 1 mol KOH:
1 N KOH * 1 L Solution = 1 equivalent = 1 mol KOH = 56.1 g KOH
b) The partial equation:
I2 + 2e– → 2I–
Indicates that 2 electrons react with the I2, therefore 2 equivalents = 1 mol or 1 equivalent = ½ mol
1 N I2 * 1 L Solution = 1 equivalent = ½ mol I2 = 253.8/2 g = 126.9 g I2
c) As the H3PO4 provides 3 H+, 3 equivalents = 1 mol, or 1 equivalent = 1/3 mol.
1 N H3PO4 * 1 L Solution = 1 equivalent = 1/3 mol H3PO4 = 98/3 g = 126.9 g H3PO4
.
B.3. Calculate the normality of each of the following solutions:
a)76 g nitric acid (HNO3) (as an acid) in 1 L of solution. Molecular mass HNO3: 63 g/mol.
b) 5 g sodium carbonate (Na2CO3) (when neutralized to form carbon dioxide (CO2)) in 1 L of solution. Molecular mass Na2CO3: 106 g/mol
Answer
a) As the HNO3 provides 1 mol of H+, 1 equivalent = 1 mol HNO3 = 63 g HNO3.
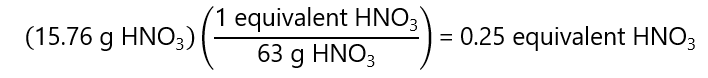
As this is in 1 L of solution, we have 0.25 equivalents / 1 L = 0.25 N HNO3.
b) The reaction of the Na2CO3 produces carbonic acid (H2CO3), however, the carbonic acid in the presence of water rapidly converts into carbon dioxide (CO2) and water. We can summarize this as:
Na2CO3 + 2H+ → H2CO3 → CO2 + H2O
Therefore, the Na2CO3 reacts with 2 H+ and 2 equivalents = 1 mol Na2CO3 = 106 g or 1 equivalent = 106 g/2 = 53 g.
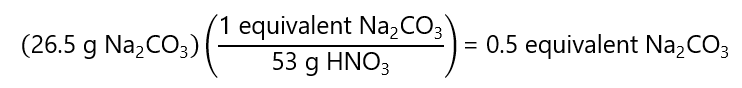
As this is in 1 L of solution, the concentration is 0.5 equivalent / 1 L = 0.5 N Na2CO3.
B.4. If 25.00 mL of acetic acid solution is titrated with 28.12 mL of 0.200 N KOH, what is the concentration of acetic acid?
Answer
N1V1 = N2V2
NAcid * 25 mL = 0.200 N * 28.12 mL
Nacid = 0.2*28.12/25 = 0.225 N
B.5. What is the normality of an acid if 22.25 mL were needed to fully neutralize 0.2503 g sodium carbonate (Na2CO3)?
Answer
We are not given the name of the acid, because we don’t need it. We know that the number of equivalents of the acid used is equal to the number of equivalents of the Na2CO3
As seen in exercise b.3. b), the Na2CO3 reacts with 2 H+ and 2 equivalents = 1 mol Na2CO3 = 106 g or 1 equivalent = 106 g/2 = 53 g. Therefore, the number of equivalents of Na2CO3 is:
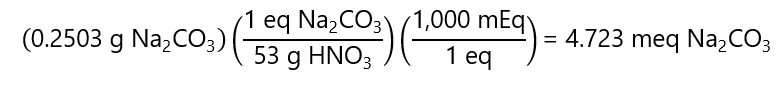
And
meq Na2CO3 = meq acid
meq Na2CO3 = Nacid * Vacid (mL)
Note: as we are using meq, the volume is given in mL
4.723 meq Na2CO3 = Nacid * 22.25 (mL)
Nacid = 4.723 / 22.25 = 0.212 N
B.6. what is the normality of a 2.50 M solution of sulfuric acid (H2SO4) in the following reactions?
a) H2SO4 + NaOH → NaHSO4 + H2O
b) H2SO4 + 2NaOH → Na2SO4 + 2H2O
c) SO42-+ 10H++ 8e–→ H2S + 4H2O
Answer
As we have seen in ‘Example 3.7’, in a) 1 eq = 1 mol, in b) 2 eq = 1 mol and in c) 8 eq = 1 mol. With these data, we can find the answers.
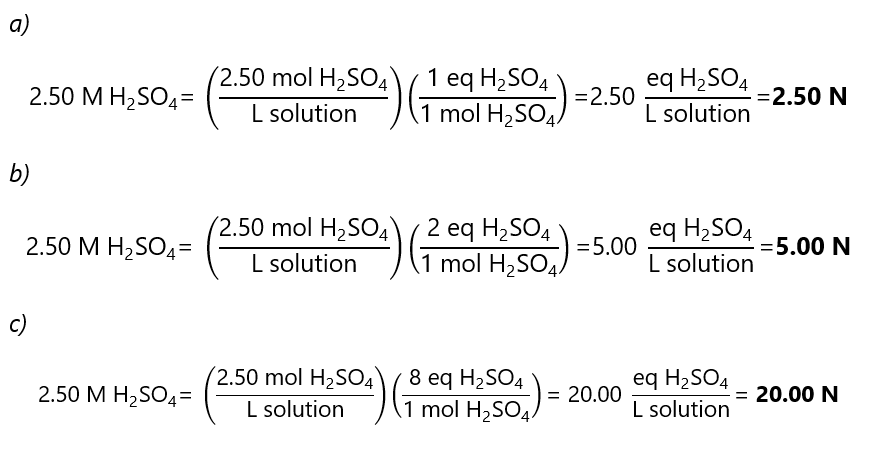
c) Molality
C.1. Calculate the molality of each of the following solutions:
a)0 g of ethanol (C2H5OH) in 210 g of water (molecular mass C2H5OH: 46.1 g/mol)
b) 0 g potassium bromide (KBr) in 100.0 g of water (molecular mass KBr: 119 g/mol
Answer
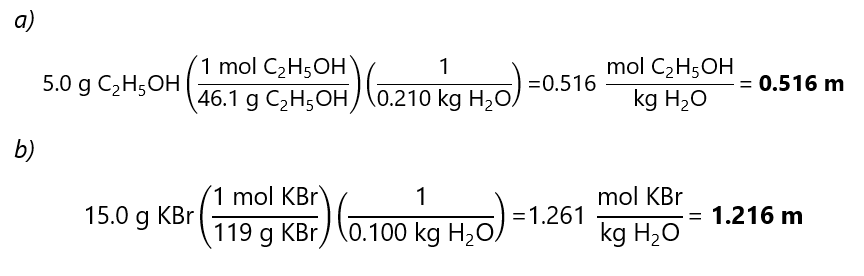
C.2. How many moles of solute are there in a 1.5 m solution containing 4.0 kg of solvent?
Answer
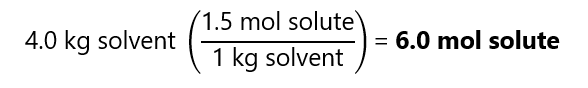
C.3. Calculate the total molality of all ions when 15.9 g of sodium carbonate (Na2CO3) is dissolved in 750 g of water. Molecular mass Na2CO3: 106 g/mol
Answer
Mol of Na2CO3
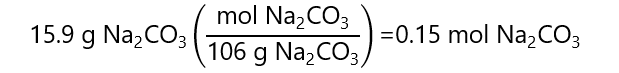
As the dissociation of 1 mol Na2CO3 produces a total of 3 mol of ions (2 mol of Na+ + 1 mol CO32-):
Na2CO3 → 2Na+ + CO32-
0.15 mol produces 3 * 0.15 = 0.45 mol of ions. Therefore
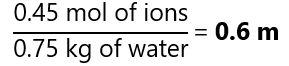
C.4. Calculate the molality of a chloride ions in a solution containing 50.0 g of magnesium chloride (MgCl2) in 500 mg of water. Molecular mass MgCl2: 95.2 g/mol.
Answer
The number of mol of MgCl2 is:
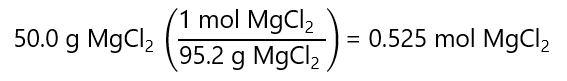
As each mol of MgCl2 provides 2 mol of Cl–, the number of mol of Cl– in solution is 0.525 * 2 = 1.050 mol Cl–. Divided by the 0.5 kg of solvent (water) gives:
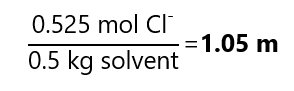
C.5. What is the molality of a solution of 5.0 g of glucose (C₆H₁₂O₆) dissolved in 125.0 g of water? Molecular mass C₆H₁₂O₆: 180.2 g/mol
Answer
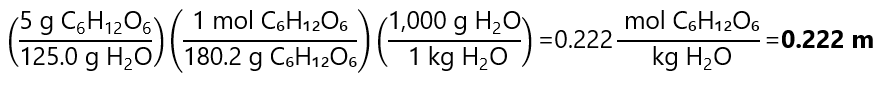
C.6. The molality of a solution of acetone (C3H6O) is 2 mol/kg. How many grams of C3H6O are dissolved in 1.5 kg of water? Molecular mass C3H6O: 58.1 g/mol.
Answer
The number of mol of C3H6O in 1.5 kg of water is:

And the mass of 3 mol of C3H6O is:
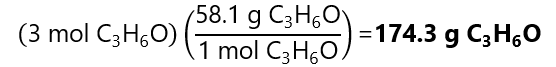
C.7. Calculate the molality of a sulfuric acid (H2SO4) solution 27% w/w and density 1.198 g/mL. Molecular mass H2SO4: 98.1 g/mol.
Answer
As there is no indication of the quantity of the sample, we consider that we use a litre of solution (we can use any other quantity but 1 L makes the calculation easier). We start by converting the mass of H2SO4 that we have in 1 L of solution:
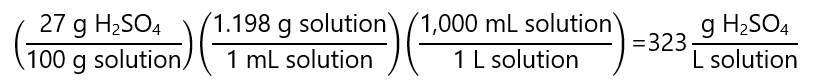
If we have 1 L of solution, from the density, we know that its mass is 1.198 kg. We also know that the H2SO4 has a mass of 323.5 g (0.323 kg), therefore the weight of the solvent (H2O) is:
Mass of H2O = mass of solution – mass of H2SO4 =
= 1.198 kg – 0.323 kg = 0.875 kg
We know the masses of the solute (H2SO4) and the solvent (H2O), we only need to transform the mass of the solute to mol:
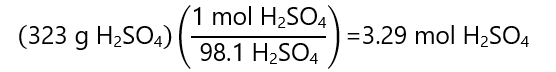
And the molality is:
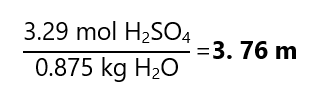
C.8. Calculate the molality of a solution prepared by adding 20.0 g of water to a 1.50 m solution containing 75.0 g of water.
Answer
The 75.0 g (0.075 kg) of the 1.50 m solution contains:
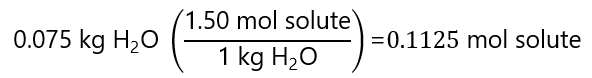
And the final mass of solvent is 75.0 g+ 20.0 g = 95.0 g = 0.095 kg. Therefore, the molality is:
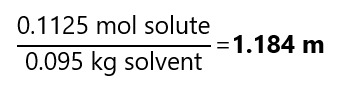
C.9. A sulfuric acid solution containing 571.4 g of H2SO4 per litre of solution has a density of 1.329 g/mL. What is the molality of the solution? Molecular mass H2SO4: 98.1 g/mol
Answer
Considering that we have 1 L of solution, we know that:
- Mass of solution: 1.329 kg (given by the density)
- Mass of solute: 571.4 g H2SO4 = 0.5714 kg H2SO4
Therefore, the mass of the solvent is the difference between the solution and the solute:
Mass solvent = mass solution – mass solute =
= 1.329 kg – 0.5714 kg = 0.7576 kg solvent
We calculate the mass of the solvent with the molar mass:
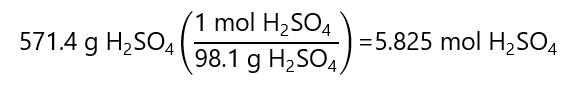
And the molality is:
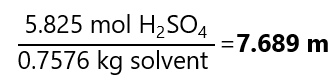
C.10. Calculate the molality of 15 M hydrochloric acid (HCl) with a density of 1.0745 g/cm3 and molecular mass: 36.5 g/mol.
Answer
As we are not given a quantity of sample, let’s take a 1L to make the calculation easier. If we have 1 L of solution and the concentration is 15 M, we have 15 mol HCl.
The next step is to calculate the mass of the solvent. We know that:
Mass of the solution = mass of the solute + mass of the solvent
The mass of the solution can be obtained from the density (remember that we are working with 1 L and 1 cm3 = 1 mL):
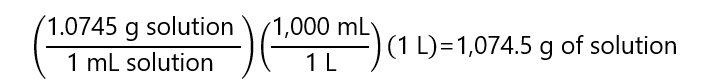
The mass of the solute can be obtained from the number of moles (15 moles HCl) and its molecular mass:
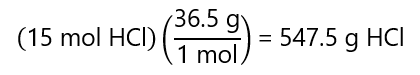
With these results, we can write:
Mass of the solution = mass of the solute + mass of the solvent
1,074.5 g = 547.5 g + mass of solvent
Mass of solvent = 1,074.5 – 547.5 = 527 g = 0.527 kg
Therefore, the molality is:
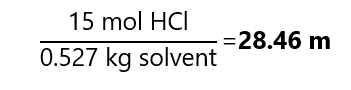
d) Mole fraction
D.1. Calculate the molar fractions of each of both substances containing 116.2 g of acetone (C3H6O, molar mass 58.1 g/mol) and 54.0 g of water (H2O molecular mass: 18.0 g/mol).
Answer
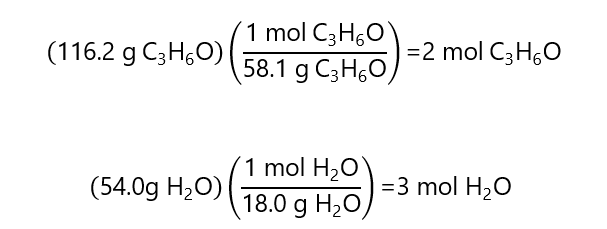
Total number of moles: 2 + 3 = 5 moles
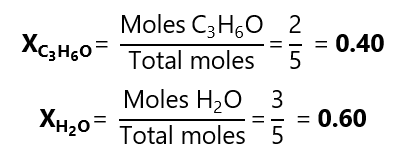
We can check that we have the right answer by adding both molar fractions and checking that it gives 1:
0.40 + 0.60 = 1
D.2. Calculate the mole fraction of each component in a solution prepared with 20.0 g of ethanol ((C2H5OH molecular mass: 46.1 g/mol) and 50.0 g of water (H2O, molecular mass water: 18.0 g/L)
Answer
The number of moles of each component is:
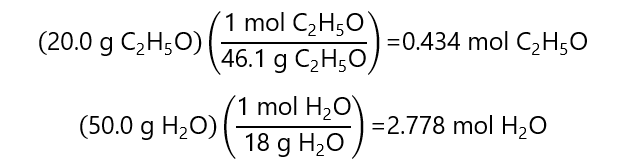
Total number of moles = 0.434 + 2.778 = 3.213 mol
And each mole fraction:
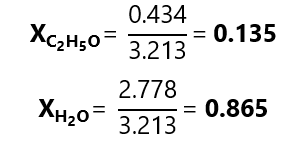
We can check that the calculations are correct as 0.135 + 0.865 = 1
D.3. Calculate the molality of a solution with a mole fraction 0.250 of ethanol (C2H5OH) in water (H2O, molecular mass water: 18.0 g/L)
Answer
As we are not given the quantity of sample, we assume that the total number of moles is 1 and therefore the number of moles of C2H5OH is 0.250 (given by the molar fraction)
Total number of moles = moles of C2H5OH + moles H2O
1 = 0.250 + moles H2O
Moles H2O = 0.750
And with the molecular mass, we find the mass of the 0.750 mol H2O:
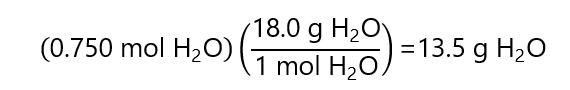
And the molality is:
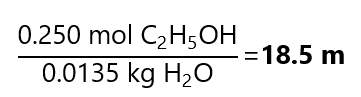
D.4. Calculate the mole fraction of a solution 0.200 m of glucose (C6H12O6) in water (H2O, molecular mass: 18.0 g/mol)
Answer
As we are not given the amount of solution, we consider that we have 1 kg of solvent, as it is 0.200 m in glucose, it means that we have 0.200 moles of glucose.
On the other hand, the number of moles of water is:
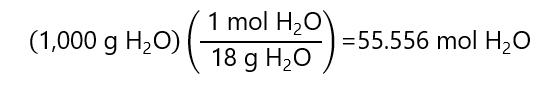
Therefore, the mole fraction is
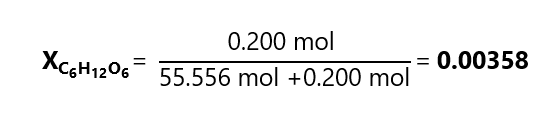
D.5. An aqueous solution is prepared by diluting 3.30 mL acetone (C3H6O) (density = 0.789 g/mL, molecular mass: 58.08 g/mol) with water to a final volume of 75.0 mL. The density of the solution is 0.993 g/mL. What is the molarity, molality and mole fraction of acetone in this solution? Molecular mass H2O: 18 g/mol.
Answer
Molarity: we know the final volume (75 mL or 0.075 L), we need to find out the number of moles acetone that can be found in 2 steps:
1. Calculation of the mass of acetone using the density
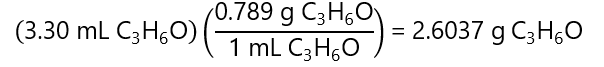
2. With the mass of acetone and its molecular mass, we find the number of moles:
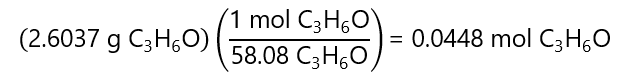
With this result, we can calculate the molarity:
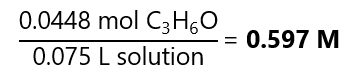
Molality: we already know the number of moles of the solute (0.0448 mol C3H6O), we need to find out the mass of the solvent. We know that:
Mass of the solution = mass of the solute + mass of the solvent
We know the mass of the solute from the molarity calculation (2.6037 g of C3H6O), the mass of the solution can be calculated with its density (0.993 g/mL) and its volume (75 mL or 0.075 L):
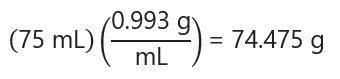
Therefore:
Mass of the solution = mass of the solute + mass of the solvent
74.475 g = 2.6037 g + mass of solvent
Mass of solvent = 74.475 – 2.6037 = 71.8713 g = 0.0718713 kg
And:
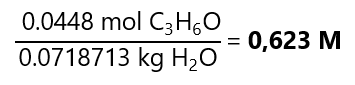
Molar fraction: we already know the number of moles of the solute (0.0448 mol C3H6O). We need to calculate the number of moles of the solvent, as we know its mass (71.8713 g H2O), we can find the number of moles using it molecular mass:
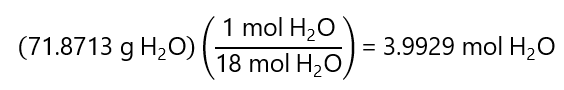
Therefore:
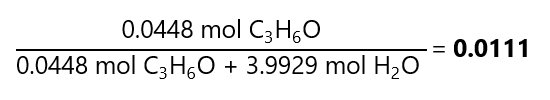
e) Concentrations expressed in physical units
E.1. How many grams of a 7.0% (w/w) sodium chloride (NaCl) solution we need if we want to obtain 2.8 g of sodium chloride?
Answer
Using the factor label method, we find that:
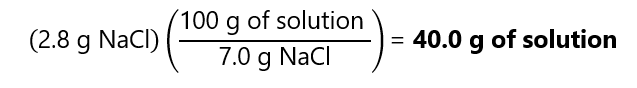
Alternatively, we can solve the equation:
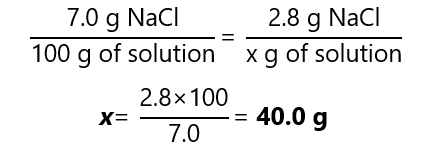
E.2. If we want to make a 50 mL of a solution containing 46 mg of Na+ / mL of solution, how many grams of sodium nitrate (NaNO3) we need to add? Molecular masses: NaNO3: 85 g/mol. Na: 23 g/mol
Answer
As we have NaNO3 and the concentration asked is in Na+, we need to transform from “mg of Na+ / mL of solution” to “mg of NaNO3 / mL of solution”. We use the fact that molecular masses can be expressed either in g/mol of mg/mmol (they are the same):
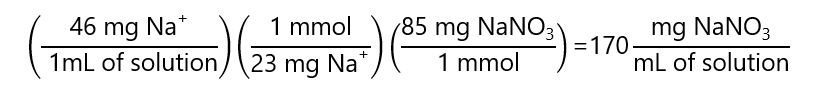
Now, we need to find how much NaNO3 we need to prepare 50 mL of this solution:
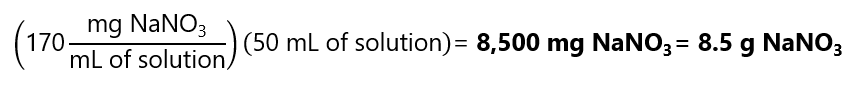
E.3 Hydrochloric acid (HCl) is commercially available as 37% w/w acid with a density of 1.18 g/ml. How many grams of anhydrous HCl we have in 50 mL of this solution?
Answer
From the density we can calculate the mass of these 50 mL of solution are:
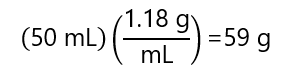
As the concentration is 37% w/w:
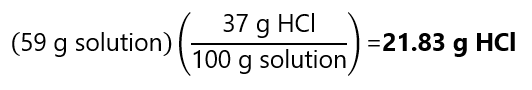
E.4. If 863 mg of ferric ammonium sulfate (FeNH4(SO4)2.12H2O) is dissolved and diluted to 500.0 mL with water, what is the concentration of iron (Fe) in ppm in the solution? Molecular masses: (FeNH4(SO4)2.12H2O): 482.2 g/mol. Fe: 55.8 g/mol.
Answer
As we have a very diluted solution (they are asking the concentration in ppm), we can express ppm as mg/kg or mg/L. Remember that molecular masses can be expressed in g/mol or mg/mol.
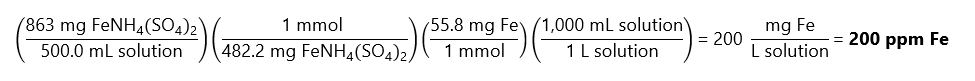
f) Dilutions
F.1. What is the concentration of a solution prepared by diluting 2 L of a 4 M NaCl solution to 9 L with water?
Answer
CiVi = CfVf
4 M x 2 L = Cf x 9 L
Cf = (4 x 2 ) / 9 = 0.89 M
F.2. What is the concentration of a solution prepared by diluting 250 mL of a 3 M solution to 600 mL?
Answer
CiVi = CfVf
3 M x 250 mL = Cf x 600 mL
Cf = (3 x 250 ) / 600 = 1.25M
F.3. How many mL of concentrated sulfuric acid (H2SO4), 98% w/w H2SO4, density 1.84 g/mL, molecular mass 98 g/mol, we need to use to prepare the following solutions:
a) 1.5 L of 1 N H2SO4?
b) 200 mL of 1.5 N H2SO4?
c) 1 L of 0.5 N H2SO4?
Answer
To be able to work with volume, we express the concentration of the H2SO4 in g/mL instead of w/w:
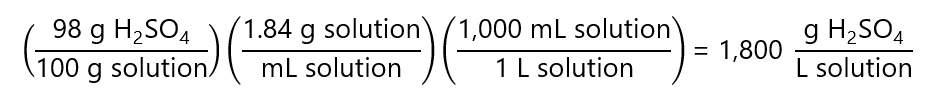
We need express this concentration in N using the number of equivalents of the H2SO4. As it provides 2 H+, we have 2 equivalents = 1 mol H2SO4 = 98 g H2SO4 or 1 equivalent = 98/2 = 49 g.
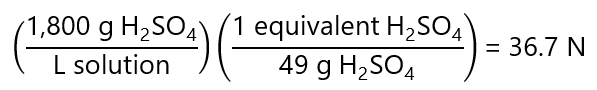
And we can now solve each question using CiVi = CfVf
a)
36.7 N * Vi = 1 N * 1.5 L
Vi = 1.5 / 36.7 = 0.0409 L = 40.9 mL
b)
36.7 N * Vi = 1.5 N * 200 mL
Ci = 1.5*200 / 36.7 = 8.2 mL
c)
36.7 N * Vi = 0.5 N * 1 L
Ci = 0.5*1 / 36.7 = 0.0136 L = 13.6 mL
F.4. What is the final concentration of hydrochloric acid (HCl) if 1.5 L of 2.4 N HCl and 2.0 L of 1.6 N HCl are mixed and diluted to 4.0 L
Answer
1.5 L * 2.4 N = 3.6 equivalents HCl
2.0 L * 1.6 N = 3.2 equivalents HCl
Total: 3.6 + 3.2 = 6.8 equivalents HCl
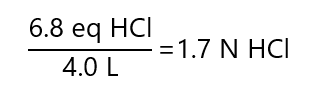
F.5. To what volume we need to dilute 1.0 mL of the 200 ppm iron (Fe) solution from exercise 5.5. to obtain a 4 ppm iron solution?
Answer
CiVi = CfVf
200 ppm x 1.0 mL = 4 ppm x Vf
Vf = (200 x 1.0 ) / 4 = 50.0 mL
We need to dilute 1.0 mL to 50.0 mL.
F.6. How many mL of an 30% v/v ammonia (NH3) solution do we need to prepare 1 L of 6 M ammonia (NH3)? Molecular mass NH3: 17 g/mol. Density: 0.9 g/mL
Answer
To obtain 1 L of 6 M NH3 I need:
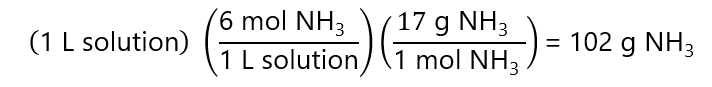
The 102 g NH3 is provided by the 30% v/v solution. The volume of 102 g of NH3:
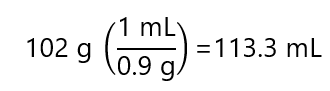
And using the concentration:
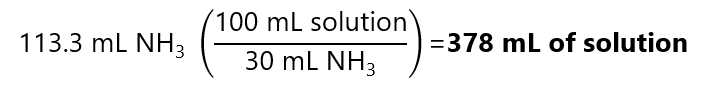
I.e. to 378 mL of the 30% solution we need to add solvent (water) to make 1 L.
