On this page, I describe how the chemical formulas are written, how to obtain them and I finish with a set of solved exercises for practice.

The outline of this chapter is:

1. Atomic theory.
2. Atomic masses and moles.
3. Molecules and molecular mass.
4. Percentage composition
5. Empirical formulas.
6. Molecular formulas.
7. Exercises.
   • Molecular mass.
   • Moles.
   • Percentage composition.
   • Empirical formulas.
   • Molecular formulas.
8. Comments

Atomic theory

During the 19^th century, the atomic theory developed. At the beginning of the century, Dalton proposed that molecules are formed by the combination of atoms. The idea was developed over the century. The main points of Dalton’s atomic theory, as it eventually developed, are:

• Elements are made of extremely small particles called atoms.
• Atoms of a given element have similar mass and properties, atoms of different elements differ in mass and properties.
• Atoms of different elements combine in simple whole-number ratios to form chemical compounds.
• In chemical reactions, atoms are combined, separated or rearranged, but not destroyed.

Atomic masses and moles

Note: You will find that sometimes in chemistry, mass(es) and weight(s) are use interchangeably. Both terms mean the same for a chemist, however, a physic will disagree. I will use the term mass or masses.

As the atomic theory was developing, the next step was to determine the masses of atoms. As the atoms are so small, they could not be measured at the time that the theory was developed and therefore it was decided to refer to a relative scale of masses between atoms and defined a new unit: the atomic mass unit (amu). Initially, it was developed using as a unit the mass of the hydrogen, however, over time it was changed to use the most common element found, that is isotope of carbon 12 (or ¹²C) and therefore:

1 atom of ¹²C = 12 amu

Based on this, the values of atomic masses were developed and are given in the periodic table.

As chemical reactions involved a considerable number of atoms, the use of amu was not very practical in real terms, therefore it was defined a new unit: the mole (abbreviated as mol). A mole is defined as the number of atoms present in 12 g of ¹²C. As science developed, it was possible to quantify the numbers of atoms in 12 g of ¹²C, this number is 6.0221 × 10²³ and is known as Avogadro’s number (N_A).

Avogadro’s number (N_A) = 6.0221 × 10²³ is the number of particles in 1 mol.

In practical terms, when we are working with atomic masses, you can use amu or g/mol.

Molecules and molecular mass

Following the atomic theory, we can define chemical species based on the atoms that constitute the compound. The nomenclature is to write the elements that constitute the molecules, indicating with a subindex the number of atoms, for example, water has the formula H₂O, meaning that it is formed by 2 atoms of hydrogen (H) and 1 atom of oxygen (O).

In nature, we have discrete molecules where the atoms are bonded by covalent bonds (like the water that we mentioned above) and other compounds where the atoms are bonded by ionic bonds, forming larger crystalline structures, like the NaCl (salt that we use in food).

This is applicable when we have discrete molecules formed by covalent bonds (like water). But there are some compounds that are not formed by single molecules, they are formed by ions than tend to form large structures, in this case, they are called ‘formula units’ and it is the simplest formulation that we can have for this compound. For example, the salt that we use in the food, is formed by crystals containing the same number of atoms of sodium (Na) and chlorine (Cl). The ‘formula unit’ of this salt is NaCl. Sometimes, formula units are referred as molecules as well, it is not technically correct, but it is a common practice.

A compound’s molecular mass (M_r, however sometimes referred to as M_w) is the sum of the atomic masses of all the atoms that appear in its formula. For example, if the atomic mass of the hydrogen is 1 g/mol and the atomic mass of oxygen is 16 g/mol, the molecular mass of the water (H₂O) is:

Molecular mass of H₂O =

= 2 x atomic mass of H + (1 x) atomic mass of O =

= 2 x 1 + 16 = 18 g/mol

The relationships between mass, molecular weight and the number of moles are:

 

 

 

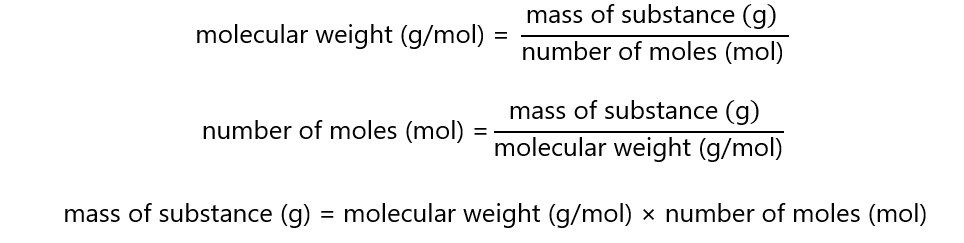
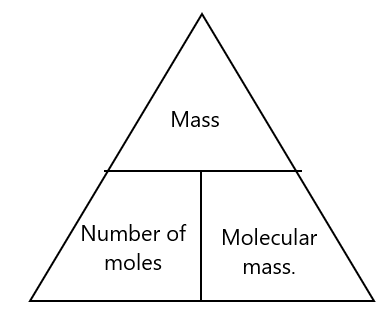
You can summarize it in the following triangle equation:

The molecular formula of sulfuric acid is H₂SO₄. a) What is it molecular mass? b) How many moles are in 500 g of H₂SO₄? c) What is the mass of 2.5 moles of H₂SO₄? The respective atomic masses are: H: 1.008 g/mol, S: 32.065 g/mol and O: 15.999 g/mol. (You can round these atomic masses to 1, 32 and 16 respectively, however, I will use 3 decimal places to minimize rounding errors).

Answer

The molecular mass of the H₂SO₄ is

2 x atomic mass of H + 1 x atomic mass of S + 4 x atomic mass of O =

= 2 x 1.008 + 1 x 32.065 + 4 x 15.999 =

= 2.016 + 32.065 + 63.996 =

= 98.077 g/mol.

To find the number of moles in 500 g of sulfuric acid, you can use proportions:

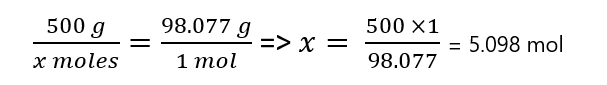
or if you prefer to work with units:

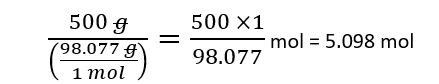
To calculate how much weight 2.5 moles of H₂SO₄, simply multiply the molecular mass by the number of moles:

2.5 mol x 98.077 g/mol = 245.193 g (rounded to 3 decimal places)

Note: When using molecular weights, there is a rounding error depending on how many decimal places you use. It will be common to have similar numbers, but not the same. For example, if instead of using 98.077 g/mol, I use 98.1 g/mol, I get that 2.5 moles weight 245.250 g (not 245.193 g). In most cases, it will not make too much difference (if accuracy is needed, the chemist has tools to achieve this accuracy at his/her disposal). For our purpose here, if you repeat the calculations by yourself or find tabulated values that are similar to those that I have, we can consider that we have the same result.

If the atomic mass of the sodium (Na) is 22.990 g/mol and the chlorine (Cl) is 35.453 g/mol:

a) What is the molecular mass of sodium chloride (NaCl)?

b) How many moles do we have in 200 g of NaCl?

c) What is the weight of 4.5 moles of NaCl?

Answers

a) The molecular is:

1 x atomic mass of Na + 1 x atomic mass of Cl =

= 1 x 22.990 + 1 x 35.453 =

= 58.443 g/mol

b) As the molecular mass is 58.443 g/mol, 200 g are:

200 g / 58.443 g/mol= 3.422 mol

c) As the molecular mass is 58.443 g/mol, 4.5 moles are:

4.5 mol x 58.443 g/mol = 262.994 g

If the atomic masses of the potassium (K) is 39.098 g/mol, the manganese (Mn) is 54.938 g/mol and the oxygen (O) is 15.999 g/mol:

a) what is the molecular mass of potassium permanganate (KMnO₄)?

b) How many moles do we have in 450 g of KMnO₄?

c) What is the weight of 1.5 moles of KMnO₄?

Answer

a) The molecular mass is:

1 x atomic mass of K + 1 x atomic mass of Mn + 4 x atomic mass of O =

= 1 x 39.083 + 1 x 54.938 + 4 x 15.999 =

= 1 x 39.083 + 1 x 54.938 + 63.996 =

= 158.032 g/mol

b) As the molecular mass is 158.032 g/mol, 450 g are:

450 g / 158.032 g/mol = 2.848 moles

c) As the molecular mass is 158.032 g/mol, 1.5 moles are:

1.5 moles x 158.032 g/mol = 237.048 g

Percentage composition

The percentage that each element contributes to the total weight of a compound is calculated by the formula:

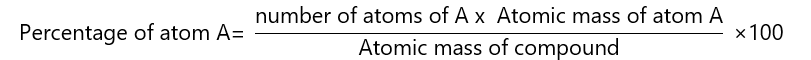
When the number of the atoms is 1, it is not usually written.

What is the percentage of potassium (K), manganese (Mn) and oxygen (O) in the potassium permanganate (KMnO₄)? Atomic masses K: 39.098 g/mol, Mn: 54.938 g/mol, O = 15.999 g/mol.

The molecular mass of the potassium permanganate (KMnO₄) is:

1 x atomic mass of K + 1 x atomic mass of Mn + 4 x atomic mass of O =

= 1 x 39.083 + 1 x 54.938 + 4 x 15.999 =

= 1 x 39.083 + 1 x 54.938 + 63.996 =

= 158.032 g/mol

The different percentages is:

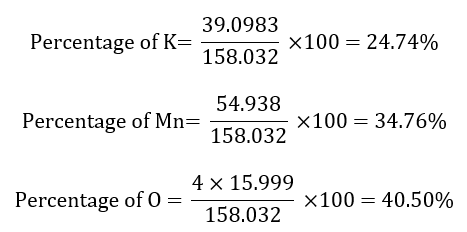
Adding all the percentages, we obtain 100%: 24.74 + 34.76 + 40.50 = 100.00. Sometimes, we get that the answer is 99.99% instead of 100.00%. Is it wrong? No, it is due to rounding errors and we can consider that the answer is correct.

Empirical formulas

Sometimes, we can only know the weights of the atoms that appear in a chemical compound. Sometimes, the results are given as percentage of weight, the process is the same: we consider that the total mass is 100 grams (or any other mass unit). How can we find what is it formula? The steps to follow are:

1. Divide the weight of each element found by its atomic mass. This will give the number of moles of each element. The same procedure can be applied if instead of weights, we have percentages (in this case, the total weight is 100 g.) IMPORTANT: use at least 2 decimal places when working with the number of moles to calculate empirical formulas, as rounding errors can lead you to the wrong answer.
2. Divide the moles of each element for the lower moles found. This will give the proportion of moles. Sometimes we need to multiply the numbers obtained to get whole numbers.

It might be helpful to create a table to develop the problem with the following headings:

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
…	…	…	…	…
…	…	…	…	…

(see the samples below to see how to fill it).

 

 

What is the empirical formula of a component that contains 60 g of sulfur and 90 g of oxygen? Atomic masses: S = 32.066 g/mol, O = 15.999 g/mol

Answer

1. We first divide the weight of each element found by its atomic mass:

% S: 60 g / 32.066 g/mol = 1.871 mol

% O: 90 g / 15.999 g/mol = 5.621 mol

2. The lower number of mols is 1.871 for the S, therefore, we divided both by 1.871:

S: 1.871 / 1.871 = 1

O: 5.621 / 1.871 = 3

Or creating a the table:

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
S	32.066	60	60 / 32.066 = 1.871	1.871/1.871 = 1
O	15.999	90	90/15.999 = 5.625	5.625/1.871 = 3

As the ratio is 3 moles of O for each mole of S, the empirical formula is SO₃.

 

What is the empirical formula of a component that contains 26.57% of potassium, 35.36% of chromium and 38.07% of oxygen? Atomic masses: K = 39.098 g/mol, Cr = 51.996, O = 15.999 g/mol.

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
K	39.098	26.57	26.57 / 39.098 = 0.680	0.680 / 0.680 = 1
Cr	51.996	35.36	35.36 / 51.996 = 0.680	0.680 / 0.680 = 1
O	15.999	38.07	38.07 / 15.999 = 2.380	2.380 / 0.680 = 3.5

This would give us the formula: KCrO_3.5, however, as the formulas are expressed in whole numbers, we multiply by 2 the contribution of each atom to obtain: K₂Cr₂O₇, (potassium dichromate).

Molecular formulas

Empirical formulas give the proportion of atoms in molecules, however, there are molecules that can have the same proportions of atoms. For example, the methane (CH₄) and the ethene (C₂H₈), both have the same proportion of atoms (4 atoms of hydrogen for each atom of hydrogen) but they have different number of atoms (5 in the methane and 10 in the ethene). When a formula gives the proportion of atoms and the total number of atoms, it is a molecular formula. To clarify:

• The empirical formula of a compound is the simplest, indicating the ratio of atoms of each element in a compound.
• The molecular formula gives the actual number of atoms of each element present in a compound.

In some cases, the empirical formula and the molecular formula are the same. Examples:

Empirical formula	Molecular formula
H2O	H2O
CO2	CO2
CH4	CH4, C2H8
NO2	N2O4
CH3O	C2H6O2
CH2O	C6H12O6

How can we find the molecular formula from the empirical formula? It is done by knowing the molecular mass of the compound. There are different ways to determine the molecular mass of compounds, however, I will not cover them here. I will explain how to determine the molecular formula from the empirical formula and the molecular mass of the molecular formula. For example, we have a sample that its empirical formula is CH₄ and its molecular mass is 32.086 g/mol. We can consider that the compound has the molecular formula (CH₄)_n(or C_nH_4n), where n is:

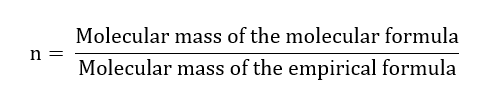
The molecular mass of the empirical formula (CH₄) is:

atomic mass of C + 4 x atomic mass of H =

= 12.011 + 4 x 1.008 =

= 16.043 g/mol

As the molecular mass of the molecular formula is 32.086 g/mol,

n = 32.086 / 16.043 = 2

Therefore, the molecular formula is C₂H_{4 x 2} = C₂H₈.

A compound with empiric formula CH₂O has a molecular mass of 180.156 g/mol. What is the molecular formula of the compound? Atomic masses: C: 12.011 g/mol, H: 1.008 g/mol, O: 15.999 g/mol.

The molecular mass empirical formula is

atomic mass of C + 2 x atomic mass of H + atomic mass of O =

= 12.011 + 2 x 1.008 + 15.999 =

= 30.026 g/mol

Therefore n = 180.156 / 30.026 = 6 and the molecular formula is (CH₂O)_n = C_nH_2nO_n = C₆H₁₂O₆

A compound is formed with 92.26% of carbon and 7.74% of hydrogen. Its molecular mass is 78.114 g/mol. Atomic masses: C: 12.011 g/mol, H: 1.008 g/mol.

We start calculating the empirical formula:

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
C	12.011	92.26	92.26 / 12.011 = 7.681	7.681 / 7.679 = 1
H	1.008	7.74	7.74 / 1.008 = 7.679	7.679 / 7.679 = 1

Therefore, the empirical formula is CH, and its molecular mass is:

atomic mass of C + atomic mass of H =

= 12.011 + 1.008 =

= 13.019 g/mol

If we divide the molecular mass of the compound by the molecular mass of the empirical formula:

n = 78.114 / 13.019 = 6

Giving the molecular formula (CH)_n = (CH)₆ = C₆H₆

Exercises

Molecular mass

1. Calculate the molecular mass of Na₂SO₄.  Atomic masses: Na: 22.990 g/mol, S: 32.066 g/mol, O: 15.999 g/mol.

Answer

 

Na: 2 x 22.990 = 45.980

 

S: 1 x 32.066 = 32.066

 

O: 4 x 15.999 = 63.996

 

Na₂SO₄ = 45,980 + 32.066 + 63.996 = 142.042 g/mol

 

---

2. Calculate the molecular mass of (NH₄)₂SO₃.  Atomic masses: N: 14.007 g/mol, H: 1.008 g/mol, S: 32.066 g/mol, O: 15.999 g/mol.

Answer

As the NH₄ appears twice, in the calculation we should count as N₂H₈SO₃

N: 2 x 14.007 = 28.014

H: 8 x 1.008 = 8,064

S: 1 x 32.066 = 32,066

O: 3 x 15.999 = 47.997

(NH₄)₂SO₃ = 28.014 + 8.064 + 32.066 + 47.997 = 116.141 g/mol

 

 

---

 

3.  Calculate the molecular mass of H₃PO₄.  Atomic masses: H: 1.008 g/mol, P: 30.974 g/mol, O: 15.999 g/mol.

Answer

H: 3 x 1.008 = 3.024

P: 1 x 30.974 = 30.974

O: 4 x 15.999 = 63.996

H₃PO₄ = 3.024 + 30.974 + 63.995 = 97.994 g/mol

 

 

 

---

 

4. Calculate the molecular mass of Hg₂(NO₃)₂.  Atomic masses: Hg: 200.59 g/mol, N: 14.007 g/mol, O: 15.999 g/mol.

Answer

As the nitrate ion (NO₃^–) appears twice, we should count as Hg₂N₂O₆

Hg: 2 x 200.59 = 401.18

N: 2 x 14.007 = 28.014

O: 6 x 15.999 = 95.994

Hg₂(NO₃)₂ = 401.18 + 28.014 + 95.994 = 525.188 g/mol

 

 

---

 

5. Calculate the molecular mass of Al₂(SO₃)₃.  Atomic masses: Al: 26.982 g/mol, S: 32.066 g/mol, O: 15.999 g/mol.

Answer

As the sulfite ion (NO₃^2-) appears three times, we should count as Al₂S₃O₉

Al: 2 x 26.982 = 53.964

S: 3 x 32.066 = 96.198

O: 9 x 15.999 = 143.991

Al₂SO₃ = 53.964 + 96.198 + 143.991 = 294.153 g/mol.

 

 

 

---

Moles

1. How many moles of is 100 g of (NH₄)₂SO₃? Atomic masses: N: 14.007 g/mol, H: 1.008 g/mol, S: 32.066 g/mol, O: 15.999 g/mol.

Answer

M_r (NH₄)₂SO₃: 2 x 14.007 + 8 x 1.008 + 1 x 32.066 + 3 x 15.999 = 116.141 g/mol

100 g of (NH₄)₂SO₃ is  100 g / 116.141 g/mol = 0.861 mol

 

 

---

 

2. How many moles of is 250 g of Na₂HPO₄? Atomic masses: Na: 22.990 g/mol, H: 1.008 g/mol, P: 30.974 g/mol, O: 15.999 g/mol.

Answer

M_r Na₂HPO₄: 2 x 22.990 + 1 x 1.008 + 1 x 30.974 + 4 x 15.999 = 141.958 g/mol

250 g of Na₂HPO₄ is 250 g / 141.958 g/mol = 1.761 mol

 

 

---

 

3. How many moles of is 400 g of KNO₃? Atomic masses: K: 39.098 g/mol, N: 14.007 g/mol, O: 15.999 g/mol

Answer

M_r KNO₃: 1 x 39.098 + 1 x 14.007 + 3 x 15.999 = 101.103 g/mol

400 g of KNO₃ is 400 g / 101.103 g/mol = 3.956 mol

 

 

---

 

4. How many moles of is 350 g of Ca(MnO₄)₂? Atomic masses: Ca: 40.078 g/mol, Mn: 54.938 g/mol, O: 15.999 g/mol

Answer

M_r Ca(MnO₄)₂: 1x 40.078 + 2 x 54.938 + 8 x 15.999 = 277.946 g/mol

350 g of Ca(MnO₄)₂ is 350 g / 277.946 g/mol = 1.259 mol

 

 

---

 

5. How many moles of is 800 g of Fe₂(SO₄)₃. Atomic masses: Fe: 55.933 g/mol, S: 32.066 g/mol, O: 15.999 g/mol

Answer

 

M_r Fe₂(SO₄)₃: 2 x 55.933 + 3 x 32.066 + 12 x 15.999 = 400.052 g/mol

800 g of Fe₂(SO₄)₃ is 800 g / 400.052 g/mol = 2.000 mol

 

 

---

 

6. What is the mass of 2 moles of NaHCO₃? Atomic masses: Na: 22.990 g/mol, H: 1.008 g/mol, C: 12.011 g/mol, O: 15.999 g/mol

Answer

M_r NHCO₃: 1 x 22.990 + 1 x 1.008 + 1 x 12.011 + 3 x 15,999 = 84.006 g/mol

2 moles of NHCO3 are 2 mol x 84.006 g/mol = 168.012 g

 

 

---

 

7. What is the mass of 2.5 moles of H₂SO₄? Atomic masses:  H: 1.008 g/mol, S: 32.066 g/mol, O: 15.999 g/mol

Answer

M_r H₂SO₄: 2 x 1.008 + 1 x 32.066 + 4 x 15,999 = 98.078 g/mol

moles of NHCO3 are 2.5 mol x 98.078 g/mol = 245.195 g

 

 

---

 

8. What is the mass of 1.5 moles of K₃PO₄? Atomic masses:  K: 39.098 g/mol, P: 30.974 g/mol, O: 15.999 g/mol

Answer

M_r K₃PO₄: 3 x 39.098 + 1 x 30.974 + 4 x 15,999 = 212.264 g/mol

1.5 moles of K₃PO₄ are 1.5 mol x 212.264 g/mol = 318.395 g

 

 

---

 

9. What is the mass of 0.5 moles of NaCN? Atomic masses:  Na: 22.990 g/mol, C: 12.011 g/mol, N: 14.007 g/mol

Answer

M_r NaCN: 1 x 22.990 + 1 x 12.011 + 1 x 14,007 = 49.008 g/mol

0.5 moles of NaCN are 0.5 mol x 49.008 g/mol = 24.504 g

 

 

---

 

10. What is the mass of 3.5 moles of HgCl₂. Atomic masses:  Hg: 200.59 g/mol, Cl: 35.453 g/mol

Answer

M_r HgCl₂: 1 x 200.59 + 2 x 35.453 = 271.496 g/mol

3.5 moles of HgCl₂ are 3.5 mol x 271.496 g/mol = 950.236 g

 

 

---

 

Percentage composition

Note: the results of the percentage are rounded to 2 decimal places.

1. Calculate the percentage composition of ammonia (NH₃). Atomic masses: N: 14.007 g/mol, H: 1.008 g/mol

Answer

 

M_r NH₃: 1 x 14.007 + 3 x 1.008 = 17.031 g/mol

 

% N: (14.007 / 17.031) x 100 = 82.24%

 

% H: (3 x 1.008 / 17.031) x 100 = 17.76%

 

Check: 82.24 + 17.76 = 100

 

---

2. Calculate the percentage composition of Ca₃(PO₄)₂. Atomic masses: Ca: 40.078 g/mol, P: 30.974 g/mol, O: 15.999 g/mol.

Answer

M_r Ca₃(PO₄)₂: 3 x 4.078 + 2 x 30.974 + 8 x 15.999 = 310.174 g/mol

% Ca: (3 x 4.078 / 310.174) x 100 = 38.76%

% P: (2 x 30.974 / 310.174) x 100 = 19.97%

 % O: (4 x 15.999 / 310.174) x 100 = 41.26%

Check: 38.76 + 19.97 + 41.26 = 99.99, it is not 100.00 due to rounding errors in the calculations. In these cases, we can consider that the solution given is correct (you can check that the result is correct by using all the decimal places when adding the results).

 

 

---

 

4. Calculate the percentage composition of butane (C₄H₁₀). Atomic masses: C: 12.011 g/mol, H: 1.008 g/mol.

Answer

M_r C₄H₁₀: 4 x 12.011 + 10 x 1.008 = 58.124 g/mol

% C: (4 x 12.011 / 58.124) x 100 = 82.66%

% H: (10 x 1.008 / 58.124) x 100 = 17.34%

Check: 82.66 + 17.34 = 100

---

5. Calculate the percentage composition of magnesium phosphate (Mg₃(PO₄)₂). Atomic masses: Mg: 24.305 g/mol, P: 30.974 g/mol, O: 15.999 g/mol

Answer

M_r Mg₃(PO₄)₂: 3 x 24.306 + 2 x 30.974 + 8 x 15.999 = 262.855 g/mol

% Mg: (3 x 24.306 / 262.855) x 100 = 27.74%

% P: (2 x 30.974 / 262.855) x 100 = 23.57%

 % O: (8 x 15.999 / 262.855) x 100 = 48.69%

Check: 27.74 + 23.57 + 48.69 = 100

 

 

---

 

6. Calculate the percentage composition of silver chromate (Ag₂CrO₄). Atomic masses: Ag: 107.868 g/mol, Cr: 51.996 g/mol, O: 15.999 g/mol

Answer

M_r Ag₂CrO₄: 2 x 107.868 + 51.996 + 4 x 15.999 = 331.728 g/mol

% Ag: (2 x 107.868 / 331.728) x 100 = 65.03%

% Cr: (51.996 / 331.728) x 100 = 15.67%%

 % O: (4 x 15.999 / 331.728) x 100 = 19.29%

Check: 65.03 + 15.67 + 19.29 = 99.99

 

 

---

 

7. Calculate the percentage composition of sodium thiosulfate pentahydrate (Na₂S₂O₃·5H₂O), Atomic masses: Na: 22.990 g/mol, S: 32.066 g/mol, O: 15.999 g/mol, H: 1.008 g/mol

Answer

We have to account for the 5 molecules of water, therefore, for the calculations we need to calculate it as: (Na₂S₂O₈H₁₀)

M_r Na₂S₂O₃·5H₂O: 2 x 22.990 + 2 x 32.066 + 8 x 15.999 + 10 x 1.008 = 248.184 g/mol

% Na: (2 x 22.990 / 248.184) x 100 = 18.53%

% S: (2 x 32.066 / 248.184) x 100 = 25.84%

 % O: (8 x 15.999 / 248.184) x 100 = 51.57%

% H: (10 x 1.008 / 248.184) x 100 = 4.06%

Check: 18.53 + 25.84 + 51.57 + 4.06 = 100

 

 

---

 

8. Calculate the percentage composition of lead acetate (Pb(C₂H₃O₂)₂). Atomic masses: Pb: 207.2 g/mol, C: 12.011 g/mol, H: 1.008 g/mol, O: 15.999 g/mol

Answer

 

M_r Pb(C₂H₃O₂)₂: 207.2 + 4 x 12.011 + 6 x 1.008 + 4 x 15.999 = 355.27 g/mol

% Pb: (207.2 / 355.27) x 100 = 58.32%

% C: (4 x 12.011 / 355.27) x 100 = 13.52%

% H: (6 x 1.008 / 355.27) x 100 = 1.13%

% O: (4 x 15.999 / 355.27) x 100 = 27.02%

Check: 58.32 + 13.52 + 1.13 + 27.02 = 99.99

 

 

---

 

9. Calculate the percentage composition of chloroform (CHCl₃). Atomic masses: C: 12.011 g/mol, H: 1.008 g/mol, Cl: 35.453 g/mol

Answer

 

M_r CHCl₃: 12.011 + 1.008 + 3 x 35.453 = 119.38 g/mol

% C: (12.011 / 119.38) x 100 = 10.06%

% H: (1.001 / 119.38) x 100 = 0.84%

% Cl: (3 X 35.453 / 119.38) x 100 = 89.09%

Check: 10.06 + 0.84 + 89.09 = 99.99

 

 

---

 

10. Calculate the percentage composition of glucose (C₆H₁₂O₆). Atomic masses: C: 12.011 g/mol, H: 1.008 g/mol, O: 15.999 g/mol.

Answer

 

M_r C₆H₁₂O₆: 6 x 12.011 + 12 x 1.008 + 6 x 15.999 = 180.160 g/mol

% C: (6 x 12.011 / 180.160) x 100 = 40.00%

% H: (12 x 1.001 / 180.160) x 100 = 6.71%

% 0: (6 x 15.999 / 180.160) x 100 = 53.28%

Check: 40.00 + 6.71 + 53.28 = 99.99

 

 

---

 

Empirical formulas

1. Calculate the empirical formula of a compound which has a percent composition Mg: 20.19%, S: 26.64%, 0: 53.17%. Atomic masses: Mg: 24.305 g/mol, S: 32.066 g/mol, O: 15.999 g/mol

Answer

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
Mg	24.305	20.19	20.19 / 24.305= 0.831	0.831 / 0831 = 1
S	32.066	26.64	26.64 / 32.066 = 0.831	0.831 / 0831 = 1
O	15.999	53.17	53.17 / 15.88 = 3.323	3.323 / 0831 = 4

Answer: MgSO₄.

 

 

---

 

2. A sample of 100.00 g of iron oxide (Fe_xO_y) has 69.98 g of iron. What is its empirical formula? Atomic masses: Fe: 55.995 g/mol, O: 15.999 g/mol.

Answer

As the sample is 100 g and it has 69.98 g of iron, the rest is oxygen: 100 – 69.98 = 30.02 g of O

 

 

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
Fe	55.995	69.98	69.98 / 55.995 = 1.251	1.251 / 1.251 = 1
O	15.999	30.02	30.02 / 15.99 = 1.876	1.876 / 1.251 = 1.50

To have whole numbers, we multiply by 2 and the answer is: Fe₂O₃.

 

 

---

 

3. A 2.000 g sample of uranium is heated in the air. The oxide formed (U_xO_y) formed weight 2.358 g. What is the empirical formula of the oxide? Atomic masses: U: 238.029 g/mol, O: 15.999 g/mol

Answer

The content of oxygen is 2.358 g – 2.000 g = 0.358 g

 

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
U	238.029	2.000	2.000 / 238.029 = 0.008	0.008 / 0.008 = 1
O	15.999	0.358	0.358 / 15.999 = 0.022	0.022 / 0.008 = 2.66

Multiplying by 3, we get U₃O₈.

 

 

---

4. A compound is made of 13.260 g of Chromium, 12.265 g of sulfur and 24.475 g of oxygen. What is its empirical formula? Atomic masses: Cr: 51.996 g/mol, S: 32.066 g/mol and O: 15.999 g/mol.

Answer

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
Cr	51.996	13.260	13.260 / 51.996 = 0.255	0.255 / 0.225 = 1
S	32.066	12.265	12.265 / 32.066 = 0.382	0.382 / 0.225 = 1.5
O	15.999	24.475	24.475 / 15.999 = 1.530	1.530 / 0.225 = 6

To have whole numbers, we multiply by 2: Cr₂S₃O₁₂. This can be rearranged as Cr₂(SO₄)₃, chromium sulfate.

 

 

---

 

5. Find the empirical formula of a compound that contains 43.38% of sodium, 11.33% of carbon and 45.29 of oxygen. Atomic masses: Na: 22.990 g/mol, C: 12.011 g/mol and O: 15.999 g/mol.

Answer

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
Na	22.990	43.38	43.38 / 22.990 = 1.887	1.887 / 0.943 = 2
C	12.011	11.33	11.33 / 12.011 = 0.943	0.943 / 0.943 = 1
O	15.999	45.29	45.29 / 15.999 = 2.831	2.831 / 0.943 = 3

The compound is Na₂CO₃, sodium carbonate.

 

 

---

 

6. Find the empirical formula of a sample of 50.000 g that has the following composition: potassium 19.525 g, hydrogen: 0.505 g, carbon: 6.000 g and oxygen: 23.970 g.  Atomic masses: K: 39.098 g/mol, H: 1.008 g/mol, C: 12.011 g/mol and O: 15.999 g/mol.

Answer

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
K	39.098	19.525	19.525 / 39.098 = 0.499	0.499 / 0.499 = 1
H	1.008	0.505	0.505 / 1.008 = 0.501	0.501 / 0.499 = 1
C	12.011	6.000	6.000 / 12.011 = 0.500	0.500 / 0.499 = 1
O	15.999	23.970	23.970 / 15.999 = 1.498	1.498 / 0.499 = 3

The sample is KHCO₃, potassium bicarbonate.

 

 

---

 

7. The combustion of 150.000 g an organic sample formed by carbon (C), hydrogen (H) and oxygen (O) combusts with oxygen to produce 260.787 g of carbon dioxide (CO₂) and 143.505 g of water (H₂O). What is the empirical formula of the sample? Atomic masses: C: 12.011 g/mol, H: 1.008 g/mol, O: 15.999 g/mol.

Answer

The non-adjusted combustion reaction of the compound is:

C_xH_yO_z + O₂ → CO₂ + H₂O

As you can see, the carbon and the hydrogen are only provided by the sample, whereas the oxygen is provided partly by the compound and partly by the oxygen present in the air stream used in the combustion. The only way to calculate the oxygen present in the formulation is by subtracting to the mass of the sample, the masses of C provided the CO₂ and the oxygen provided by the H₂O:

Mass of O = mass of sample – mass of C – mass of H

Let’s go by parts.

We start with the C:

• • • • The molecular mass of CO₂ is 1 x 12.011 + 2 x 15.999 = 44.009 g/mol.
      • The atomic mass of the C is 12.011 g/mol.
      • Therefore, the proportion in masses between CO₂ and the C is:

Mass of CO₂ / Mass of C = 44.009 / 12.011

 

• • • • As the sample provides 260.787 g of CO₂, we have the following equation:

(Mass of CO₂ / Mass of C =) 44.009 / 12.011 = 260.787 / mass of carbon

• • • • That leads to:

mass of carbon = 12.011 x 260.787 / 44.009 = 71.029 g

 

Now the hydrogen: 

• • • • The molecular mass of H₂O is 2 x 1.008 + 15.999 = 18.015 g/mol.
      • The atomic mass of the H is 1.008 g/mol and in each molecule of H2O we have 2 hydrogens, their contribution is 1.008 x 2 = 2.016
      • Therefore, the proportion in masses between H₂O and the H is:

mass H₂O / mass of H = 18.015 / 2.016

 

• • • • As the sample provides 143.505 g of H₂O, we have the following equation:

(mass H₂O / mass of H =) 18.015 / 2.016 = 143.505 / mass of H

 

• • • • That leads to:

mass of H= 143.505 x 2.016 / 18.015 = 16.059 g.

 

This means that:

Mass of O = mass of sample – mass of C – mass of H =

= 150.000 – 71.029 – 16.059 =

= 62.912 g

 

With these numbers, we can proceed as before:

 

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
C	12.011	71.029	71.029 / 12.011 = 5.914	5.914 / 3.932 = 1.50
H	1.008	16.095	16.095 / 1.008 = 15.967	15.967 / 3.932 = 4.06
O	15.999	62.912	62.912 / 15.999 = 3.932	3.932 / 3.932 = 1.00

We multiply by 2 to get whole numbers and the answer is: C₃H₈O₂.

 

 

---

 

8. The combustion of 200.000 g an organic sample formed by carbon (C), hydrogen (H) and oxygen (O) combusts with oxygen to produce 382.114 g of carbon dioxide (CO₂) and 234.626 g of water (H₂O). What is the empirical formula of the sample? Atomic masses: C: 12.011 g/mol, H: 1.008 g/mol, O: 15.999 g/mol.

Answer

The procedure is the same that seen in the previous exercise. The non-adjusted combustion reaction of the compound is:

C_xH_yO_z + O₂ → CO₂ + H₂O

To calculate the mass of oxygen, we subtract to the mass of the sample, the masses of C provided the CO₂ and the oxygen provided by the H₂O:

Mass of O = mass of sample – mass of C – mass of H

If we proceed like the previous exercise, we can find that

• • As the sample provides 382.114 g of CO₂, we have the following equation:

(Mass of CO₂ / Mass of C =) 44.009 / 12.011 = 382.114 / mass of carbon

 

This means:

mass of carbon = 44.009 / 12.011 = 382.114 x 12.011 / 44.099 = 104.287 g

 

• • As the sample provides 234.626 g of H₂O, we have the following equation:

(mass H₂O / mass of H =) 18.015 / 2.016 = 234.626 / mass of H

This means:

mass of H = 234.626 x 2.016 / 18.015 = 26.256 g 

• • And total mass of carbon is:

Mass of O = mass of sample – mass of C – mass of H =

= 200.000 – 104.287 – 26.256 =

= 69.457 g

With these numbers:

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
C	12.011	104.287	104.287 / 12,011 = 8.683	8.6831 / 4.341 = 2.00
H	1.008	26.256	26.256 / 1.008 = 26.048	26.048 / 4.341 = 6.00
O	15.999	69.457	69.457 / 15.999 = 4.341	4.341 / 4.341 = 1.00

The answer is: C₂H₆O.

 

 

---

 

Molecular formulas

1. A sugar contains 40.00% carbon, 6.71% of hydrogen and 53.28% of oxygen. If the molecular mass of the compound is 150.130 g/mol, calculate its molecular formula. Atomic masses: C: 12.011 g/mol, H: 1.008 g/mol, O: 15.999 g/mol.

Answer

We start by calculating the empirical formula:

 

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
C	12.011	40.00	40.00 / 12.011 = 3.330	3.330 / 3.330 = 1
H	1.008	6.71	6.71 / 1.008 = 6.657	6.657 / 3.330 = 2
O	15.999	53.28	53.28 /15.999 = 3.330	3.330 / 3.330 = 1

The empirical formula is CH₂O, its molecular mass is:

atomic mass of C + 2 x atomic mass of H + atomic mass of O =

= 12.011 + 2 x 1.008 + 15.999 =

= 30.026 g/mol

 The molecular formula is (CH₂O)_n, with

n = 150.130 / 30.026 = 5

The molecular formula is: C₅H₁₀O₅.

 

 

---

 

2. An hydrocarbon contains 85.63% of carbon and its molecular mass is 84.162 g/mol. What is its molecular formula? Atomic masses: C: 12.011 g/mol, H: 1.008 g/mol.

Answer

The first step is to calculate the percentage of hydrogen.

100.00 – 85.63 = 14.37 % of hydrogen.

We then calculate the molecular formula:

 

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
C	12.011	85.63	85.63 / 12.011 = 7.129	7.129 / 7.129 = 1
H	1.008	14.37	14.37 / 1.008 = 14.256	14.256 / 7.129 = 2

The molecular formula is CH₂, its molecular mass is:

atomic mass of C + 2 x atomic mass of H =

= 12.011 + 2 x 1.008  =

= 14.027 g/mol

 The molecular formula is (CH₂)_n, with

n = 84.162 / 14.027 = 6

The molecular formula is: C₆H₁₂.

 

 

---

 

3. White or chrysotile asbestos is made of magnesium (28.03%), silicone (21.60%), hydrogen (1.16%) and oxygen (49.21%) O. Its molar mass is 520.206 g/mol. What is its molecular formula? Atomic masses: Mg: 24.305 g/mol, Si: 28.086 g/mol, H: 1.008 g/mol and O: 15.999g/mol.

Answer

We start by calculating the empirical formula:

 

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
Mg	24.305	28.03	28.03 / 24.305 = 1.153	1.153 / 0.769 = 1.50
Si	28.086	21.60	21.60 / 28.086 = 0.769	0.769 / 0.769 = 1.00
H	1.008	1.16	1.16 / 1.008 = 1.151	1.151 / 0.769 = 1.50
O	15.999	49.21	48.21 / 15.999 = 3.076	3.076 / 0.769 = 4.00

To have whole numbers, we multiply by 2 and the empirical formula is Mg₃Si₂H₃O₈, its molecular mass is:

3 x atomic mass of Mg + 2 x atomic mass of Si + 3 x atomic mass of H + 8 x atomic mass of O =

= 3 x 24.305 + 2 x 28.086 + 3 x 1.008 + 8 x 15.999 =

= 260.103 g/mol

 The molecular formula is (Mg₃Si₂H₃O₈)_n, with

n = 260.103 / 520.206 = 2

The molecular formula is: Mg₆Si₄H₆O₁₆.

 

 

---

 

4. Yellow acridine yellow has a percent composition of carbon: 75.92%, hydrogen: 6.37% and nitrogen: 17.71% with a molar mass of about 237.306 g/mol. Determine its molecular formula. Atomic masses: C: 12.011 g/mol, H: 1.008 g/mol and N: 14.007 g/mol.

Answer

Calculation of the empirical formula:

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
C	12.011	75.92	75.92 / 12.011 = 6.321	6.321 / 1.264 = 5.00
H	1.008	6.37	6.37 / 1.008 = 6.319	6.321 / 1.264 = 5.00
N	14.007	17.71	17.71 / 14.007 = 1.264	1.264 / 1.264 = 1.00

The empirical formula is C₅H₅N with molecular mass:

 5 x atomic mass of C + 5 x atomic mass of H + atomic mass of N =

= 5 x 12.011 + 5 x 1.008 +14.007 =

= 79.102 g/mol

The molecular formula is (C₅H₅N)_n, with

n = 237.306 / 79.102 = 3

The molecular formula is: C₁₅H₁₅N₃.

 

 

---

 

5. The combustion of 250.000 g an organic sample formed by carbon (C), hydrogen (H) and oxygen (O) combusts with oxygen to produce 568.298 g of carbon dioxide (CO₂) and 232.632 g of water (H₂O). What is the molecular formula of the sample if its atomic mass is 116.160 g/mol? Atomic masses: C: 12.011 g/mol, H: 1.008 g/mol, O: 15.999 g/mol.

Answer

The non-adjusted combustion reaction of the compound is:

C_xH_yO_z + O₂ → CO₂ + H₂O

As you can see, the carbon and the hydrogen are only provided by the sample, whereas the oxygen is provided partly by the compound and partly by the oxygen present in the air stream used in the combustion. The only way to calculate the oxygen present in the formulation is by subtracting to the mass of the sample, the masses of C provided the CO₂ and the oxygen provided by the H₂O:

Mass of O = mass of sample – mass of C – mass of H

Let’s go by parts.

We start with the C:

• • • The molecular mass of CO₂ is 1 x 12.011 + 2 x 15.999 = 44.009 g/mol.
    • The atomic mass of the C is 12.011 g/mol.
    • Therefore, the proportion in masses between CO₂ and the C is:

Mass of CO₂ / mass of C = 44.099/12.011

• • • As the sample provides 568.298 g of CO2, we have the following equation: 

(Mass of CO₂ / mass of C =) 44.099/12.011 = 568.298 / mass of C

• • • That leads to:

mass of C = 468.298 x 12.011 / 44.099 = 155.101 g

Now the hydrogen:

• • The molecular mass of H₂O is 2 x 1.008 + 15.999 = 18.015 g/mol.
  • The atomic mass of the H is 1.008 g/mol and in each molecule of H2O we have 2 hydrogens, their contribution is 1.008 x 2 = 2.016
  • Therefore, the proportion in masses between H₂O and the H is:

mass H₂O / mass H = 18.015/ 2.016

• • As the sample provides 232.632 g of H₂O, we have the following equation:

(mass H₂O / mass H =) 18.015/ 2.016 = 232.632 / mass of H

• • That leads to:

mass of H = 232.632 x 2.015 / 18.015 = 26.033 g

This means that:

Mass of O = mass of sample – mass of C – mass of H =

= 250.000 – 155.101 – 26.033 =

= 68.866 g

With this numbers, we can proceed as before:

 

Atom	Atomic mass	Mass (or %)	Number of moles (mass/atomic mass)	Number of moles/lowest number of moles
C	12.011	155.101	155.101 / 12.011 = 12.913	12.913 / 4.304 = 3
H	1.008	26.033	26.033 / 1.008 = 25.826	25.826 / 4.304 = 6
O	15.999	68.866	68.866 / 15.999 = 4.304	4.304 / 4.304 = 1

Therefore, the empirical formula is C₃H₆O, its molecular mass is:

3 x atomic mass of C + 6 x atomic mass of H + atomic mass of O =

= 3 x 12.011 + 6 x 1.008  + 15.999=

= 58.080 g/mol

 The molecular formula is (C₃H₆O)_n, with

n = 116.160 / 58.080 = 2

The molecular formula is: C₆H₁₂O₂.

 

 

---

 

Comments

If you have any question, or want to add anything else, please leave a comment below.