On this page, I explain how to balance reduction-oxidation (redox) chemical equations. You should be familiarized with the basic balancing equations, which I explain in this link.

Outline for this page:

• Redox equations
• Oxidation states
• Steps to adjust redox equations
  • In neutral solutions
  • In acidic aqueous solutions
  • In basic (alkaline) aqueous solutions
• Exercises
• Comments

Redox equations

I have created a video explaining how to balance redox equations. You can watch it by clicking here.

These reactions are more complex than simple reactions. You will see then after you have seen the simple reactions. In these reactions, the oxidation states of the atoms change (more below). In some cases, the equations can be solved as shown in the simple equations, however, on other cases (like ionic equations in aqueous solutions) it is simpler to use half equations (as it is used in redox equations).

A Redox reaction is a reaction that involve the transfer of electrons between 2 species. For example:

2Na(s) + Cl₂(g) → 2NaCl(s)

It is a redox equation, where the Na loses an electron:

Na → Na⁺ + 1e^–

And the Cl gains an electron:

Cl₂ + 2e^– → 2Cl^–

Definitions:

• Oxidation: is the reaction of losing electrons (eg: Na → Na⁺ + 1e^–)
• Reduction: is the reaction of gaining electrons (eg: Cl₂ + 2e^– → 2Cl^–)
• Oxidant, oxidizing agent or oxidizer is a component that oxidize other elements (in the example, the Cl₂ is the oxidant of the Na)
• Reducer or reducing agent is a component that reduce other elements (in the example, the Na is the reducer of the Cl₂)

To easy memorize the definition of Oxidation and Reduction is to use the mnemonic word OIL RIG:

OIL RIG: Oxidation Is Losing, Reduction Is Gaining.

The 2 most common methods to balance redox equation are the oxidation number and the ion-electron method. I personally find the latter easier, as it is more systematic and can solve more complex equations.

Oxidation state

Oxidation state is the hypothetical charge of an atom if all of its bond to other atoms were fully ionic. The oxidation state is used to balance ionic equations. The following rules simplify the determination of the oxidation state:

1. The oxidation state of an individual atom is zero (as it has not been oxidised or reduced yet). For example, Cl₂, Fe, H₂, S₈ have all oxidation state zero
2. The sum of the oxidation states of all the atoms or ions in a neutral compound is zero.
3. The sum of the oxidation states of all the atoms in an ion is equal to the charge of the ion.
4. The more electronegative element in a substance is given a negative oxidation state. The less electronegative one is given a positive oxidation state. (Fluorine is the most electronegative element followed by oxygen). A table with the electronegativities of the different elements can be found at Electronegativities of the elements (data page) – Wikipedia,
5. Fluorine: always -1
6. Oxygen its oxidation state is -2, except in the peroxides and oxygen fluorides that is -1
   • Peroxides (like H₂O₂, Na₂O₂, BaO₂, …), where the 2 atoms of Oxygen are linked together (R-O-O-R) and the oxidation estate is -1
   • Oxygen fluorides (like OF₂O, O₂F₂, …): as the Fluorine is more electronegative that the Oxygen, the Oxygen the oxidation state is -1
7. Chlorine: usually -1. Except in compounds with oxygen and fluorine, in these cases it is better to work out, as its oxidation states can be +1 (case of Cl₂O), +3 (case of NaClO₂), +4 (case of ClO₂), +5 (case of NaClO₃) and +7 (Cl₂O₇)
8. Group 1, alkali metals, (when part of a molecule) has the oxidation state +1 (there are very rare exceptions to this rule and form what is known as ‘Alkalide’, discovered in 1974 by Prof James L Dye[1], for most common purposes, the rule of + 1 applies)
9. Group 2, alkali earth metals, the oxidation estate is +2

---

[1] J. L. Dye; J. M. Ceraso; Mei Lok Tak; B. L. Barnett; F. J. Tehan (1974). “Crystalline salt of the sodium anion (Na−)”. Journal of the American Chemical Society 96 (2): 608–609

---

Examples to find oxidation states:

1. Find the oxidation state of the sulphur in sulfuric acid, H₂SO₄.

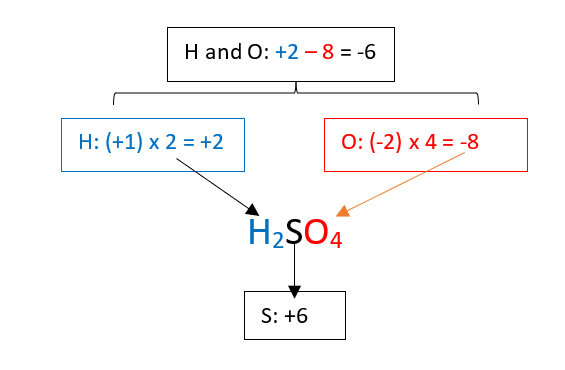
• As we have 2 hydrogen atoms, each with an oxidation state (+1), therefore, their total contribution is (+1) x 2 = +2
• As we have 4 oxygen atoms, each with an oxidation state (-2), therefore their total contribution is (-2) x 4 = -8
• The total contribution of hydrogen and oxygen atoms is + 2 – 8 = -6
• As the molecule is neutral, then, the sulphur needs to compensate for -6, therefore it oxidation state is +6

I find sometimes easier to use a mathematical equation to find the oxidation states (calling x to the unknown):

Total oxidation state of H + Total oxidation state of S + Total oxidation state of O = Total oxidation state H₂SO₄

2(+1) + x + 4(-2) = 0

2 + x – 8 = 0

x = 8 – 2

x = +6

Answer: +6

---

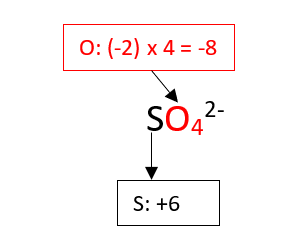
2. Find the oxidation state of the sulfur in the sulfate ion, SO₄^2-.

As seen in the previous example, the total contribution of the oxygen is -8 and the total charge of the ion is -2 (there are no hydrogen atoms on this ion). Therefore, the S compensate only for 6 negative charges, this means that its oxidation state is +6.

Or using again a mathematical equation:

Total oxidation state of S + Total oxidation state of O = Total oxidation state SO₄^2-

x + 4(-2) = -2

x – 8 = 0

x = 8 – 2

x = +6

Answer: +6

---

3. Find oxidation state of chromium in calcium dichromate, CaCr₂O₇

• The calcium has an oxidation state of +2, as it is only 1 atom of calcium, its total contribution is therefore: (+2) x 1 = +2
• There are 7 atoms of oxygen, each with an oxidation state of -2, therefore their total contribution is (-2) x 7 = -14
• The total contribution of the calcium and oxygen atoms is +2 – 14 = -12
• As the molecule is neutral, the 2 atoms of chromium need to compensate the charge of -12, therefore, each chromium has an oxidation state of +6

Or using again a mathematical equation:

Total oxidation state of Ca + Total oxidation state of Cr + Total oxidation state O = Total oxidation state CaCr₂O₇

1(+2) + 2x + 7(-2) = 0

2 + 2x – 14 = 0

2x = 14 – 2

2x = +12

x = +12/2

x = +6

Answer: +6

---

4. Find the oxidation state of chlorine in magnesium chloride, MgCl₂.

• The atom of magnesium has an oxidation state of +2
• As the magnesium chloride is neutral, the 2 atoms of chlorine need to compensate the +2 from the magnesium, therefore each atom of chloride has an oxidation state of -1

Or using a mathematical equation:

Total oxidation state of Mg + Total oxidation state of Cl = Total oxidation state MgCl₂

1(+2) + 2x = 0

2 + 2x = 0

2x = – 2

x = -2/2

x = -1

Answer: -1

---

5. Find the oxidation state of chlorine in the chlorous acid, HClO₂

This is one example where the chlorine has an oxidation state different of -1, as the oxygen is more electronegative than the chlorine, the oxygen takes the electrons from the chlorine.

• Hydrogen: 1 atom with an oxidation state +1
• Oxygen: 2 atoms, each with an oxidation (-2) therefore their contribution is 2 x (-2) = -4
• The oxygen and hydrogen atoms have a total contribution of 1 – 4 = -3
• As the chlorous acid is neutral, the chlorine has an oxidation state of +3 (to compensate the -3 from the oxygen and hydrogen atoms)

Or using a mathematical equation:

Total oxidation state of H + Total oxidation state of Cl + Total oxidation state O = Total oxidation state HClO₂

1(+1) + x + 2(-2)= 0

1 + x -4 = 0

x = +4 -1

x = +3

Answer: +3

---

Steps to adjust redox reactions

The steps to follow will depend on if the reaction is taking place in a neutral solution, in acidic aqueous solutions or in basic (alkaline) aqueous solutions. The straighter forward method is in case of neutral solutions, the other two cases require additional steps.

In neutral solutions

These are the easiest to adjust, and you can treat them as simple reactions, i.e. don’t need to use half-equations. The steps are:

1. Identify the elements that are reduced and oxidised. Write their half-reaction (i.e.: the reduction reaction and oxidation reaction) balancing the elements in the reaction and the relevant number of electrons (in the oxidation reaction the electrons will appear as products and in the reduction reaction the electron will appear as reactants)
2. Adjust both half-equations to ensure that the number of electrons are the same.
3. Add both half-equations
4. The same number of electrons should appear as reactants than as products, cancelling each other.

Example

Balance the following:

Cu⁺(aq) + Fe(s) → Fe³⁺(aq) + Cu(s)

In this example the cupric ion (Cu⁺) is reduced to copper (Cu) and the iron (Fe) is oxidised to ferric ion (Fe³⁺). The half-equations are:

Cu⁺(aq) + 1e^–→ Cu(s)

Fe(s) →Fe³⁺(aq) + 3e^–

To balance the electrons in both equations, we multiply by 3 the copper reaction:

3Cu⁺(aq) + 3e^–→ 3Cu(s)

Now we add both half-equations:

3Cu⁺(aq) + 3e^–→ 3Cu(s)

Fe(s) →Fe³⁺(aq) + 3e^–

———————————————————

3Cu⁺(aq) + 3e^–+ Fe(s)→ 3Cu(s) + Fe³⁺(aq) + 3e^–

Cancelling the electrons in both sides:

3Cu⁺(aq) + Fe(s)→ 3Cu(s) + Fe³⁺(aq)

Let’s check that the equation is balanced:

Atom	Number in reactants	Number in products
Cu	3	3
Fe	1	1
Charges	3+	3+

In acidic aqueous solutions

In these equations we are going to add, in this order, water (H₂O), hydrogen ions (also referred as protons, H⁺) and electrons (e^–)

1. Identify the elements that are reduced and oxidised.
2. Write their half-reaction balancing the elements except for the hydrogen (H) and the oxygen (O).
3. Balance the oxygen atoms by adding the appropriate number of water (H₂O) molecules to the opposite side of the equation.
4. Balance the hydrogen atoms (including those added in the previous step) by adding protons (H⁺) to the opposite side of the equation.
5. Add up the charges on each side and add electrons (e^–) to equalize the charges in both sides of each half-equation.
6. Compare the number of electrons in each half-equation, if the number is different, multiply by a convenient number (it helps to find the lowest common multiple) to make them equal.
7. Add both half-equations
8. Cancel the electrons (that should be the same number on both sides)
9. Cancel any common terms in reactants and in products

Example

Balance the reaction in acidic solution of MnO₄^–(aq) + I^– (aq) → Mn²⁺(aq) + I₂(s)

Identification of the reduction and oxidation half-reactions

Reduction: MnO₄^–(aq) → Mn²⁺(aq)

(The manganese changes from oxidation state +7 to +2)

Oxidation: I^–(aq) → I₂(s)

 (The iodine changes from oxidation state -1 to 0)

 Balancing the number of atoms, except for the H and O:

Reduction: MnO₄^–(aq) → Mn²⁺(aq)

(There is one manganese on each side of the equation)

Oxidation: 2I^–(aq) → I₂(s)

(I need 2 iodine ions to form 1 molecule of iodine)

Balancing the O, where it is necessary, by adding H₂O:

Reduction: MnO₄^–(aq) → Mn²⁺(aq) + 4H₂O(l)

(I need 4 atoms of oxygen in the products)

Oxidation: 2I^–(aq) → I₂(s)

(No oxygen in this half-equation)

Balancing the H, where it is necessary, by adding H⁺:

Reduction: MnO₄^–(aq) + 8H⁺(aq) → Mn²⁺(aq) + 4H₂O(l)

(I need 8 atoms of hydrogen in the reactants)

Oxidation: 2I^–(aq) → I₂(s)

(No oxygen in this half-equation)

Balancing the charges in each half-equation by adding e^–:

Reduction: MnO₄^–(aq) + 8H⁺(aq) + 5e^–→ Mn²⁺(aq) + 4H₂O(l)

(Reactants have a total charge of 7+, the products 2+, to balance both sides, we need to add 5 e^– to the reactants and have both sides a total charge of 2+)

Oxidation: 2I^–(aq) → I₂(s) + 2e^–

(Reactants have a total charge of 0, the products 2-, to balance both sides, we need to add 2 e^– to the products and have both sides a total charge of 2-)

Making the electrons of each half-equation equal^–:

Reduction: (multiplying by 2): 2MnO₄^–(aq) + 16H⁺(aq) + 10e^–→ 2Mn²⁺(aq) + 8H₂O(l)

Oxidation: (multiplying by 5): 10I^–(aq) → 5I₂(s) + 10e^–

(Multiplying by 2 the reduction half-equation (2 is the number of electrons in the oxidation half-equation) and by 5 the oxidation half-equation (5 is the number of electrons in the reduction half-equation) I obtain 10 electrons on both half-equations)

Adding both half-equations equal^–:

Reduction: 2MnO₄^–(aq) + 16H⁺(aq) + 10e^–→ 2Mn²⁺(aq) + 8H₂O(l)

Oxidation: 10I^–(aq) → 5I₂(s) + 10e^–

———————————————————————————

Result: 2MnO₄^–(aq) + 16H⁺(aq) + 10e^– + 10I(aq)^– → 2Mn²⁺(aq) + 8H₂O(l) + 5I₂(s) + 10e^–

Cancelling electrons (10 on each side)

2MnO₄^–(aq) + 16H⁺(aq) + 10e^– + 10I(aq)^– → 2Mn²⁺(aq) + 8H₂O(l) + 5I₂(s) + 10e-

2MnO₄^–(aq) + 16H⁺(aq)  + 10I^–(aq) → 2Mn²⁺(aq) + 8H₂O(l) + 5I₂(s)

There are no other common terms to cancel

Let’s check the number of atoms and charges:

Atom	Number in reactants	Number in products
Mn	2	2
O	8	8
H	16	16
I	10	10
Charges	4+	4+

In basic (alkaline) aqueous solutions

The steps are the same than in the acidic solution until step 9 (cancelling common terms on both sides of the equation). The steps to follow are:

1. Identify the elements that are reduced and oxidised.
2. Write their half-reaction balancing the elements except for the hydrogen (H) and the oxygen (O).
3. Balance the oxygen atoms by adding the appropriate number of water (H₂O) molecules to the opposite side of the equation.
4. Balance the hydrogen atoms (including those added in the previous step) by adding protons (H⁺) to the opposite side of the equation.
5. Add up the charges on each side and add electrons (e^–) to equalize the charges in both sides of each half-equation.
6. Compare the number of electrons in each half-equation, if the number is different, multiply by a convenient number to made them equal.
7. Add both half-equations
8. Cancel the electrons (that should be the same number in both sides)
9. Add, in both sides of the equation, as many OH^– (hydroxide ions) as H⁺ there are in the final equation.
10. Each OH^– and each H⁺ on the same side of the equation cancel each other to form 1 molecule of H₂O. This should leave the final equation with OH^– and H₂O and no H⁺ (if this is not the case, review what was done in the previous step)
11. Cancel any other common terms in reactants and in products

Note: an alternative method to this is to balance the oxygen (step 3) by adding H₂O and OH^–, excess of H⁺ are balanced by adding more OH^–, however, I found this alternative method more complex on some occasions, the method described above is more straight forward.

Example

Balance the reaction in basic solution of Ag(s) + Zn²⁺(aq) → Ag₂O(aq) + Zn(s)

Identification of the reduction and oxidation half-reactions

Reduction: Zn²⁺(aq) → Zn(s)

(The zinc changes from oxidation state +2 to 0)

Oxidation: Ag(s) → Ag₂O(aq)

 (The silver changes from oxidation 0 to +1)

Balancing the number of atoms, except for the H and O:

Reduction: Zn²⁺(aq) → Zn(s)

(The zinc is balanced)

Oxidation: 2Ag(s) → Ag₂O(aq)

 (We need to atoms of silver as reactant)

Balancing the O, where it is necessary, by adding H₂O:

Reduction: Zn²⁺(aq) → Zn(s)

(No oxygen is required with the zinc)

Oxidation: 2Ag(s) + H₂O(l)→ Ag₂O(aq)

 (As in the products we have 1 oxygen, we add 1 molecule of water as reactant)

Balancing the H, where it is necessary, by adding H⁺:

Reduction: Zn²⁺(aq) → Zn(s)

(No hydrogen is required with the zinc)

Oxidation: 2Ag(s) + H₂O(l) → Ag₂O(aq) + 2H⁺(aq)

 (As in the reactants we have 2 hydrogens and none in the products, we add 2 H⁺ in the products)

Balancing the charges in each half-equation by adding e^–:

Reduction: Zn²⁺(aq) + 2e^– → Zn(s)

(We have 2 positive charges in the reactants and no charges in the products. We balance it by adding 2 electrons in the reactants)

Oxidation: 2Ag(s) + H₂O(l) → Ag₂O(aq) + 2H⁺(aq) + 2e^–

 (As in the reactants we have no charges in the products 2 positive charges, we balance the equation by adding 2 electrons in the products)

Making the electrons of each half-equation equal^–:

Reduction: Zn²⁺(aq) + 2e^– → Zn(s)

Oxidation: 2Ag(s) + H₂O → Ag₂O(aq) + 2H⁺(aq) + 2e^–

(In both equations we have the same number of electrons, not need to modify)

Adding both half-equations equal^–:

Reduction: Zn²⁺(aq) + 2e^– → Zn(s)

Oxidation: 2Ag(s) + H₂O → Ag₂O(aq) + 2H⁺(aq) + 2e^–

———————————————————————————————–

Result: Zn²⁺(aq) + 2e^– + 2Ag(s) + H₂O → Zn(s) + Ag₂O(aq) + 2H⁺(aq) + 2e^–

Cancelling electrons (2 on each side)

Zn²⁺(aq) + 2e^– + 2Ag(s) + H₂O → Zn(s) + Ag₂O(aq) + 2H⁺ + 2e-

Zn²⁺(aq) + 2Ag(s) + H₂O → Zn(s) + Ag₂O(aq) + 2H⁺(aq)

Adding OH^‑ to compensate for the H⁺

Zn²⁺(aq) + 2Ag(s) + H₂O + 2OH^‑(aq) → Zn(s) + Ag₂O(aq) + 2H⁺(aq) + 2OH^‑(aq)

(As we have 2 H⁺ as products, we add 2 OH^– in the products and in the reactants)

Forming 1 molecule of H₂O with each OH^– and each H⁺ on the same side of the equation

Zn²⁺(aq) + 2Ag(s) + H₂O + 2OH^‑(aq) → Zn(s) + Ag₂O(aq) + 2H₂O(l)

                 (As we have 2 H⁺ and 2 OH^– in the products, we form 2 H₂0)

Cancelling common terms

Zn²⁺(aq) + 2Ag(s) + H₂O(l) + 2OH^‑(aq) → Zn(s) + Ag₂O(aq) + 2H₂O(l) + H₂O(l)

(We have 1 molecule of water as reactant and 2 molecules of water as product, we cancel 1 molecule of water in the products)

Result:

Zn²⁺(aq) + 2Ag(s) + 2OH^‑(aq) → Zn(s) + Ag₂O(aq) + H₂O(l)

Checking the atoms and charges:

Atom	Number in reactants	Number in products
Zn	1	1
Ag	2	2
O	4	4
H	2	2
Charges	0	0

---

Exercises

List of exercises. Click in the number of the exercise to go to the exercise.

Number	Question	Answer	Type
1	S2O32-(aq) + I3–(aq) → S4O62-(aq) + I–(aq)	2S2O32-(aq) + I3–(aq) → S4O62-(aq) + 3I–(aq)	Neutral
2	Cr2O72-(aq) + NO2–(aq) → Cr3+(aq) + NO3−(aq)	Cr2O72-(aq) + 3NO2–(aq) + 8H+(aq) →2Cr3+(aq) + 3NO3−(aq) + 4H2O(l)	Acid
3	Fe2+(aq) + MnO4–(aq) → 5Fe3+(aq) + Mn2+(aq)	5Fe2+(aq) + MnO4–(aq) + 8H+(aq) → 5Fe3+(aq) + Mn2+(aq) + 4H2O(l)	Acid
4	MnO4−(aq) + I−(aq) → I2 (s)+ Mn2+(aq)	2MnO4−(aq) + 16H+(aq) + 10I−(aq)→ 2Mn2+(aq) + 5I2(s) + 8H2O(l)	Acid
5	MnO4−(aq) + I−(aq) → I2 (s)+ Mn2+(aq)	2MnO4−(aq) + 8H2O(l)  + 10I−(aq)→ 2Mn2+(aq) + 5I2(s) + 16OH– (aq)	Base
6	Cr2O72−(aq)+ C2H5OH(l) → Cr3+(aq) + CO2(g)	2Cr2O72− (aq)+ 16H+(aq) + C2H5OH(l) → 4Cr3+(aq) + 11H2O(l) + 2CO2(g)	Acid.
7	Cr2O72−(aq) + C2H5OH(l) → Cr3+(aq) + CO2(g)	2Cr2O72−(aq)+ 5H2O(l) + C2H5OH(l) → 4Cr3+ + 16OH–(aq)+ 2CO2(g)	Base
8	Cl2(g) → Cl–(aq) + ClO3–(aq)	3H2O(l) + 3Cl2(g) → 5Cl­–(aq) + ClO3­–(aq) + 6H+(aq)	Acid
9	Cl2(g) → Cl–(aq) + ClO3–(aq)	6OH–(aq) + 3Cl2(g) → 5Cl­–(aq) + ClO3­–(aq) + 3H2O(l)	Basic
10	MnO4–(aq) + H2C2O4(aq) → Mn2+(aq) + CO2(g)	2MnO4–(aq) + 5H2C2O4(aq) + 6H+(aq) → 2Mn2+(aq) + 8H2O(aq) + 10CO2(g)	Acid
11	Cr2O72-(aq) + Fe2+(aq) → Cr3+(aq) + Fe3+(aq)	Cr2O72-(aq) + 6Fe2+(aq) + 14H+(aq) → 2Cr3+(aq) + 6Fe3+(aq) + 7H2O(l)	Acid
12	MnO4–(aq) + H2SO3(aq) → Mn2+(aq) + SO42-(aq)	2MnO4–(aq) + 5H2SO3(aq) → 2Mn2+(aq) + 5SO42-(aq) + 3H2O(l) + 4H+(aq)	Acid
13	MnO4–(aq) + SO32-(aq) → MnO2(s) + SO42-(aq)	2MnO4–(aq) + 3SO32-(aq) + H2O(l) → 2MnO2(s) + 3SO42-(aq) + 2OH–(aq)	Base
14	MnO4–(aq) + Br–(aq) → MnO2(s) + BrO3–(aq)	2MnO4–(aq) + Br–(aq) + H2O(l) → 2MnO2(s) + BrO3–(aq) + 2OH–(aq)	Base
15	Cu(s) + NO3–(aq) → Cu2+(aq) + NO(g)	3Cu(aq) + 2NO3–(aq) + 8H+(aq) → 3Cu2+(aq) + 2NO(g) + 4H2O(l)	Acid
16	SO42-(aq) + Zn(s) → H2S(g) + Zn2+(aq)	SO42-(aq) + 4Zn(s) + 10H+(aq) → H2S(g) + 4Zn2-(aq) + 4H2O(l)	Acid
17	SO42-(aq) + Cu(s) → SO2(g) + Cu2+(aq)	SO42–(aq) + Cu(s) + 4H+(aq) → SO2(g) + Cu2+(aq) + 2H2O(l)	Acid

1. Balance the equation S₂O₃^2-(aq) + I₃^–(aq) → S₄O₆^2-(aq) + I^–(aq) in neutral conditions

Answer: 2S₂O₃^2-(aq) + I₃^–(aq) → S₄O₆^2-(aq) + 3I^–

Half equations:

Oxidation:          2S₂O₃^2-(aq) → S₄O₆^2-(aq) + 2e^–

Reduction:         I₃^–(aq) + 2e^–→3I^–(aq)

As the electron are already equalized, we can add both equations

2S₂O₃^2-(aq) → S₄O₆^2-(aq) + 2e^–

 I₃^–(aq) + 2e^–→3I^–(aq)

————————————————-

2S₂O₃^2-(aq) + I₃^–(aq) + 2e^–→ S₄O₆^2-(aq) + 2e^–(aq)+ 3I^–

And cancel the electrons:

2S₂O₃^2-(aq) + I₃^–(aq) → S₄O₆^2-(aq) + 3I^–

Atom	Number in reactants	Number in products
S	4	4
O	6	6
I	3	3
Charges	5	5

Back to list of exercises

---

2. Balance the equation in acidic conditions: Cr₂O₇^2-(aq) + NO₂^–(aq) →Cr³⁺(aq) + NO^3-(aq)

Answer: Cr₂O₇^2-(aq) + 3NO₂^–(aq) + 8H⁺(aq) →2Cr³⁺(aq) + 3NO₃⁻(aq) + 4H₂O(l)

Half equations:

Reduction:         Cr₂O₇^2-(aq) →Cr³⁺(aq)

Oxidation:          NO₂^–(aq) → NO₃⁻(aq)

Adjusting elements except O and H:

Reduction:         Cr₂O₇^2-(aq) →2Cr³⁺(aq)

Oxidation:          NO₂^–(aq) → NO⁻³(aq)

Adjusting O by adding H₂O:

Reduction:         Cr₂O₇^2-(aq) →2Cr³⁺(aq) + 7 H₂O(l)

Oxidation:          H₂O(l) + NO₂^–(aq) → NO₃⁻(aq)

Adjusting H by adding H⁺:

Reduction:         14H⁺(aq) + Cr₂O₇^2-(aq) → 2Cr³⁺(aq) + 7H₂O(l)

Oxidation:          H₂O(l) + NO₂^–(aq) → NO₃⁻(aq) + 2H⁺(aq)

Equalizing charges by adding e^–:

Reduction:         14H⁺(aq) + Cr₂O₇^2-(aq) + 6e^– →2Cr³⁺(aq) + 7H₂O(l)

Oxidation:          H₂O(l) + NO₂^–(aq) → NO₃⁻(aq) + 2H⁺(aq) + 2e^–

Equalizing electrons in both half-equations:

Reduction:         14H⁺(aq) + Cr₂O₇^2-(aq) + 6e^– →2Cr³⁺(aq) + 7H₂O(l)

Oxidation:          3H₂O(l) + 3NO₂^–(aq) → 3NO₃⁻(aq) + 6H⁺(aq) + 6e^–

Adding both half-equations:

Reduction:         14H⁺(aq) + Cr₂O₇^2-(aq) + 6e^– →2Cr³⁺(aq) + 7H₂O(l)

Oxidation:          3H₂O(l) + 3NO₂^–(aq) → 3NO₃⁻(aq) + 6H⁺(aq) + 6e^–

———————————————————————————

Full equation: 14H⁺(aq) + Cr₂O₇^2-(aq) + 6e^– + 3H₂O(l) + 3NO₂^–(aq) →2Cr³⁺(aq) + 7H₂O(l) + 3NO₃⁻(aq) + 6H⁺(aq) + 6e^–

Cancelling electrons

14H⁺(aq) + Cr₂O₇^2-(aq) + 6e^– + 3H₂O(l) + 3NO₂^–(aq) →2Cr³⁺(aq) + 7H₂O(l) + 3NO₃⁻(aq) + 6H⁺(aq) + 6e^–

14H⁺(aq) + Cr₂O₇^2-(aq)  + 3H₂O(l) + 3NO₂^–(aq) →2Cr³⁺(aq) + 7H₂O(l) + 3NO₃⁻(aq) + 6H⁺(aq)

Cancelling common terms:

14H⁺(aq) + Cr₂O₇^2-(aq) + 3H₂O(l) + 3NO₂^–(aq) →2Cr³⁺(aq) + 7H₂O(l) + 3NO₃⁻(aq) + 6H⁺(aq)

8H⁺(aq) + Cr₂O₇^2-(aq) + 3NO₂^–(aq) →2Cr³⁺(aq) + 4H₂O(l) + 3NO₃⁻(aq)

We obtain:

8H⁺(aq) + Cr₂O₇^2-(aq) + 3NO₂^–(aq) →2Cr³⁺(aq) + 4H₂O(l) + 3NO₃⁻(aq)

The equation is balanced, but I prefer to leave H⁺ and H₂O at the end, therefore I rearrange the equation 

 Cr₂O₇^2-(aq) + 3NO₂^–(aq) + 8H⁺(aq) →2Cr³⁺(aq) + 3NO₃⁻(aq) + 4H₂O(l)

Atom	Number in reactants	Number in products
Cr	2	2
O	7 + 3×2 =13	4 + 3×3 = 9
N	3	3
H	8	4×2 = 8
Charges	8-2-3 =3+	3×2 – 3 = 3+

Back to list of exercises

---

3. Balance the equation in acidic conditions: MnO₄^–(aq) + Fe²⁺(aq) → Mn²⁺(aq) + Fe³⁺(aq)

Answer: 5Fe²⁺(aq) + MnO₄^–(aq) + 8H⁺(aq) → 5Fe³⁺(aq) + Mn²⁺(aq) + 4H₂O(l)

Half equations:

Oxidation: Fe²⁺(aq) → Fe³⁺(aq)

Reduction: MnO₄^–(aq) → Mn²⁺(aq)

Adjusting O by adding H₂O:

Oxidation: Fe²⁺(aq) → Fe³⁺(aq)

Reduction: MnO₄^–(aq) → Mn²⁺(aq) + 4H₂O(l)

Adjusting H by adding H⁺:

Oxidation: Fe²⁺(aq) → Fe³⁺(aq)

Reduction: MnO₄^–(aq) + 8H⁺(aq)→ Mn²⁺(aq) + 4H₂O(l)

Adjusting charges by adding e^–:

Oxidation: Fe²⁺(aq) → Fe³⁺(aq) + 1e^–

Reduction: MnO₄^–(aq) + 8H⁺(aq) + 5e^–→ Mn²⁺(aq) + 4H₂O(l)

Equalizing electrons:

Oxidation: 5 x (Fe²⁺(aq) → Fe³⁺(aq) + 1e^–)

5Fe²⁺(aq) → 5Fe³⁺(aq) + 5e^–

Reduction: 1 x (MnO₄^–(aq) + 8H⁺(aq) + 5e^–→ Mn²⁺(aq) + 4H₂O(l))

MnO₄^–(aq) + 8H⁺(aq) + 5e^–→ Mn²⁺(aq) + 4H₂O(l)

Adding half-equations:

Oxidation: 5Fe²⁺(aq) → 5Fe³⁺(aq) + 5e^–

Reduction: MnO₄^–(aq) + 8H⁺(aq) + 5e^–→ Mn²⁺(aq) + 4H₂O(l)

——————————————————————————-

Equation: 5Fe²⁺(aq) + MnO₄^–(aq) + 8H⁺(aq) + 5e^–→ 5Fe³⁺(aq) + 5e^– + Mn²⁺(aq) + 4H₂O(l)

Eliminating electrons and common terms:

5Fe²⁺(aq) + MnO₄^–(aq) + 8H⁺(aq) + 5e^– → 5Fe³⁺(aq) + 5e^– + Mn²⁺(aq) + 4H₂O(l)

Result:

5Fe²⁺(aq) + MnO₄^–(aq) + 8H⁺(aq) → 5Fe³⁺(aq) + Mn²⁺(aq) + 4H₂O(l)

Atom	Number in reactants	Number in products
Fe	5	5
Mn	1	1
O	4	4
H	8	4×2 = 8
Charges	5×2 – 1 + 8 = 17+	5×3 + 2 = 17+

Back to list of exercises

---

4. Balance in acidic conditions the reaction: MnO₄⁻(aq) + I⁻(aq) → I₂ (s)+ Mn²⁺(aq)

Answer: 2MnO₄⁻(aq) + 16H⁺(aq) + 10I⁻(aq)→ 2Mn²⁺(aq) + 5I₂(s) + 8H₂O(l)

Half reactions:

Reduction:          MnO₄⁻ → Mn²⁺

Oxidation:          I⁻ → I₂

Adjusting elements except O and H:

Reduction:          MnO₄⁻ → Mn²⁺

Oxidation:          2I⁻ → I₂

Adjusting O by adding H₂O:

Reduction:          MnO₄⁻ → Mn²⁺ + 4H₂O

Oxidation:          2I⁻ → I₂

Adjusting H by adding H⁺:

Reduction:          MnO₄⁻ + 8H⁺ → Mn²⁺ + 4H₂O

Oxidation:          2I⁻ → I₂

Equalizing charges by adding e^–:

Reduction:          MnO₄⁻ + 8H⁺ + 5e^–→ Mn²⁺ + 4H₂O

Oxidation:          2I⁻ → I₂ + 2e^–

Equalizing electrons in both half-equations:

Reduction:          2 x (MnO₄⁻ + 8H⁺ + 5e^–→ Mn²⁺ + 4H₂O)

2MnO₄⁻ + 16H⁺ + 10e^–→ 2Mn²⁺ + 8H₂O

Oxidation:          5 x (2I⁻ → I₂ + 2e^–)

10I⁻ → 5I₂ + 10e^–

Adding both half-equations:

Reduction:       2MnO₄⁻ + 16H⁺ + 10e^–→ 2Mn²⁺ + 8H₂O

Oxidation:        10I⁻ → 5I₂ + 10e^–

————————————————————-

Full equation:  2MnO₄⁻ + 16H⁺ + 10e^– + 10I⁻→ 2Mn²⁺ + 8H₂O + 5I₂ + 10e^–

Cancelling electrons common terms(there are no other common terms to cancel):

2MnO₄⁻ + 16H⁺ + 10e^– + 10I⁻→ 2Mn²⁺ + 8H₂O + 5I₂ + 10e^–

Result

2MnO₄⁻ + 16H⁺ + 10I⁻→ 2Mn²⁺ + 8H₂O + 5I₂

Atom	Number in reactants	Number in products
Mn	2	2
O	8	8
H	16	16
I	10	10
Charges	4+	4+

Back to list of exercises

---

5. Balance in basic (alkaline) conditions the reaction: MnO₄⁻ + I⁻ → I₂ + Mn²⁺

Answer: 2MnO₄⁻(aq) + 8H₂O(l)  + 10I⁻(aq)→ 2Mn²⁺(aq) + 5I₂(s) + 16OH^– (aq)

The equation to balance is the same than in exercise 4, but we have changed the conditions from acid to basic. As you can see, the steps are the same, but we modify the final equation by adding, in both sides of the equation, as many OH^– as H⁺ there are in the final equation.

Half reactions:

Reduction:          MnO₄⁻ → Mn²⁺

Oxidation:          I⁻ → I₂

Adjusting elements except O and H:

Reduction:          MnO₄⁻ → Mn²⁺

Oxidation:          2I⁻ → I₂

Adjusting O by adding H₂O:

Reduction:          MnO₄⁻ → Mn²⁺ + 4H₂O

Oxidation:          2I⁻ → I₂

Adjusting H by adding H⁺:

Reduction:          MnO₄⁻ + 8H⁺ → Mn²⁺ + 4H₂O

Oxidation:          2I⁻ → I₂

Equalizing charges by adding e^–:

Reduction:          MnO₄⁻ + 8H⁺ + 5e^–→ Mn²⁺ + 4H₂O

Oxidation:          2I⁻ → I₂ + 2e^–

Equalizing electrons in both half-equations:

Reduction:          2 x (MnO₄⁻ + 8H⁺ + 5e^–→ Mn²⁺ + 4H₂O)

2MnO₄⁻ + 16H⁺ + 10e^–→ 2Mn²⁺ + 8H₂O

Oxidation:          5 x (2I⁻ → I₂ + 2e^–)

10I⁻ → 5I₂ + 10e^–

Adding both half-equations:

Reduction:       2MnO₄⁻ + 16H⁺ + 10e^–→ 2Mn²⁺ + 8H₂O

Oxidation:        10I⁻ → 5I₂ + 10e^–

————————————————————-

Full equation:  2MnO₄⁻ + 16H⁺ + 10e^– + 10I⁻→ 2Mn²⁺ + 8H₂O + 5I₂ + 10e^–

Cancelling electrons common terms(there are no other common terms to cancel):

2MnO₄⁻ + 16H⁺ + 10e^– + 10I⁻→ 2Mn²⁺ + 8H₂O + 5I₂ + 10e^–

Result

2MnO₄⁻ + 16H⁺ + 10I⁻→ 2Mn²⁺ + 8H₂O + 5I₂

The additional steps, as it is alkaline conditions, is to add, in both sides of the equation, as many OH^– as H⁺ there are in the final equation. As we have 16H⁺, we add 16OH^–:

2MnO₄⁻ + 16H⁺ + 16OH^– + 10I⁻→ 2Mn²⁺ + 8H₂O + 16OH^– + 5I₂

On the left we have “16H⁺ + 16OH^– ” that will react giving water: 16H⁺ + 16OH^– → 16H₂O 

2MnO₄⁻ + 16H₂O  + 10I⁻→ 2Mn²⁺ + 8H₂O + 16OH^– + 5I₂

Eliminating the excess of water: 

2MnO₄⁻ + 16H₂O  + 10I⁻→ 2Mn²⁺ + 8H₂O + 16OH^– + 5I₂

2MnO₄⁻ + 8H₂O  + 10I⁻→ 2Mn²⁺  + 16OH^– + 5I₂

Therefore the answer is:

2MnO₄⁻ + 8H₂O  + 10I⁻→ 2Mn²⁺ + 16OH^– + 5I₂

Checking that the balance is correct:

Atom	Number in reactants	Number in products
Mn	2	2
O	16	16
H	16	16
I	10	10
Charges	12-	12-

Back to list of exercises

---

6. Balance in acidic conditions Cr₂O₇²⁻(aq) + C₂H₅OH(l) → Cr³⁺(aq) + CO₂(g)

Answer: 2Cr₂O₇²⁻ + 16H⁺ + C₂H₅OH → 4Cr³⁺ + 11H₂O + 2CO₂

Half reactions:

Reduction:          Cr₂O₇²⁻ → Cr³⁺

Oxidation:          C₂H₅OH → CO₂

Adjusting elements except O and H:

Reduction:          Cr₂O₇²⁻ → 2Cr³⁺

Oxidation:          C₂H₅OH → 2CO₂

Adjusting O by adding H₂O:

Reduction:          Cr₂O₇²⁻ → 2Cr³⁺ + 7H₂O

Oxidation:          C₂H₅OH + 3H₂O → 2CO₂

Adjusting H by adding H⁺:

Reduction:          Cr₂O₇²⁻ + 14H⁺→ 2Cr³⁺ + 7H₂O

Oxidation:          C₂H₅OH + 3H₂O→ 2CO₂ + 12H⁺

Equalizing charges by adding e^–:

Reduction:          Cr₂O₇²⁻ + 14H⁺ + 6e^–→ 2Cr³⁺ + 7H₂O

Oxidation:          C₂H₅OH + 3H₂O → 2CO₂ + 12H⁺+ 12e^–

Equalizing electrons in both half-equations:

Reduction:          2x(Cr₂O₇²⁻ + 14H⁺ + 6e^–→ 2Cr³⁺ + 7H₂O)

2Cr₂O₇²⁻ + 28H⁺ + 12e^–→ 4Cr³⁺ + 14H₂O

Oxidation:          C₂H₅OH + 3H₂O → 2CO₂ + 12H⁺+ 12e^–

Adding both half-equations:

Reduction:          2Cr₂O₇²⁻ + 28H⁺ + 12e^–→ 4Cr³⁺ + 14H₂O

Oxidation:        C₂H₅OH + 3H₂O → 2CO₂ + 12H⁺+ 12e^–

————————————————————————

Full equation:  2Cr₂O₇²⁻ + 28H⁺ + 12e^– + C₂H₅OH + 3H₂O → 4Cr³⁺ + 14H₂O 2CO₂ + 12H⁺+ 12e

Cancelling electrons common terms:

2Cr₂O₇²⁻ + 28H⁺ + 12e^– + C₂H₅OH + 3H₂O → 4Cr³⁺ + 11H₂O + 2CO₂ + 12H⁺+ 12e

2Cr₂O₇²⁻ + 16H⁺ + C₂H₅OH → 4Cr³⁺ + 11H₂O + 2CO₂

Result:

2Cr₂O₇²⁻ + 16H⁺ + C₂H₅OH → 4Cr³⁺ + 11H₂O + 2CO₂

Atom	Number in reactants	Number in products
Cr	4	4
O	15	15
H	22	22
C	2	2
Charges	12+	12+

Back to list of exercises

---

7. Balance in basic conditions Cr₂O₇²⁻(aq) + C₂H₅OH(l) → Cr³⁺(aq) + CO₂(g)

Answer: 2Cr₂O₇²⁻(aq)+ 5H₂O(l) + C₂H₅OH(l) → 4Cr³⁺ + 16OH^–(aq)+ 2CO₂(g)

The steps are the same than in exercise 6, with additional steps after we obtain the final answer. Refer to exercise 6 to see the development until the final result:

2Cr₂O₇²⁻ + 16H⁺ + C₂H₅OH + 3H₂O → 4Cr³⁺ + 14H₂O + 2CO₂

The additional steps, as it is alkaline conditions, is to add, in both sides of the equation, as many OH^– as H⁺ there are in the final equation. As we have 16H⁺, we add 16OH^–:

2Cr₂O₇²⁻ + 16H⁺ + 16OH^–+ C₂H₅OH + 3H₂O → 4Cr³⁺ + 14H₂O + + 16OH^–+ 2CO₂

As 16H⁺ + 16OH^– → H₂0

2Cr₂O₇²⁻ + 16H₂O + C₂H₅OH + 3H₂O → 4Cr³⁺ + 14H₂O +  16OH^–+ 2CO₂

We eliminate the excess of water:

2Cr₂O₇²⁻ + 16H₂O + C₂H₅OH + 3H₂O → 4Cr³⁺ + 14H₂O +  16OH^–+ 2CO₂

2Cr₂O₇²⁻ + 5H₂O + C₂H₅OH  → 4Cr³⁺ + 14H₂O +  16OH^–+ 2CO₂

Result: 2Cr₂O₇²⁻ + 5H₂O + C₂H₅OH  → 4Cr³⁺  +  16OH^–+ 2CO₂

Atom	Number in reactants	Number in products
Cr	4	4
O	20	20
H	16	16
C	2	2
Charges	4-	4-

Back to list of exercises

---

8. Balance in acidic conditions Cl₂(g) → Cl^–(aq) + ClO₃^–(aq)

This is a case of disproportionation or dismutation, in which one compound of intermediate oxidation state converts to two compounds, one of higher and one of lower oxidation states

Answer: 3H₂O(l) + 3Cl₂(g) → 5Cl­^–(aq) + ClO₃­^–(aq) + 6H⁺(aq)

Half reactions:

Reduction:          Cl₂ → Cl­^–

Oxidation:           Cl₂ → ClO₃­^–

Adjusting elements except O and H:

Reduction:          Cl₂ → 2Cl­^–

Oxidation:           Cl₂ → 2ClO₃­^–

Adjusting O by adding H₂O:

Reduction:          Cl₂ → 2Cl­^–

Oxidation:           6H₂O + Cl₂ → 2ClO₃­^–

Adjusting H by adding H⁺:

Reduction:          Cl₂ → 2Cl­^–

Oxidation:           6H₂O + Cl₂ → 2ClO₃­^– + 12H⁺

Equalizing charges by adding e^–:

Reduction:          2e^– + Cl₂ → 2Cl­^–

Oxidation:           6H₂O + Cl₂ → 2ClO₃­^– + 12H⁺ + 10e^–

Equalizing electrons in both half-equations:

Reduction:          5 x (2e^– + Cl₂ → 2Cl­^–)

10e^– + 5Cl₂ → 10Cl­^–

Oxidation:           6H₂O + Cl₂ → 2ClO₃­^– + 12H⁺ + 10e^–

Adding both half-equations:

Reduction:          10e^– + 5Cl₂ → 10Cl­^–

Oxidation:           6H₂O + Cl₂ → 2ClO₃­^– + 12H⁺ + 10e ^–

———————————————————

Full equation:  10e^– + 5Cl₂  + 6H₂O + Cl₂ → 10Cl­^– 2ClO₃­^– + 12H⁺ + 10e ^–

Cancelling electrons and common terms:

10e^– + 5Cl₂ + 6H₂O + Cl₂ → 10Cl­^– + 2ClO₃­^– + 12H⁺ + 10e ^–

6H₂O + 6Cl₂ → 10Cl­^– + 2ClO₃­^– + 12H⁺

As all the coefficients are even, we can divide by 2 all of them and have a more simplified version:

3H₂O + 3Cl₂ → 5Cl­^– + ClO₃­^– + 6H⁺

Result: 3H₂O + 3Cl₂ → 5Cl­^– + ClO₃­^– + 6H⁺

Atom	Number in reactants	Number in products
Cl	6	6
H	6	6
O	3	3
Charges	0	0

Back to list of exercises

---

9. Balance in basic conditions Cl₂(g) → Cl^–(aq) + ClO₃^–(aq)

Answer: 6OH^–(aq)+ 3Cl₂(g) → 5Cl­^–(aq) + ClO₃­^–(aq) + 3H₂O(l)

This is a case of disproportionation or dismutation, in which one compound of intermediate oxidation state converts to two compounds, one of higher and one of lower oxidation states. The steps are the same than the previous exercise, where we have the answer:

3H₂O + 3Cl₂ → 5Cl­^– + ClO₃­^– + 6H⁺

Adding OH^– in each side of the equation as H⁺ we have:

6OH^– + 3H₂O + 3Cl₂ → 5Cl­^– + ClO₃­^– + 6H⁺ + 6OH^–

Forming H₂O from H⁺ and OH^–:

6OH^– + 3H₂O + 3Cl₂ → 5Cl­^– + ClO₃­^– + 6H⁺ + 6OH^–

6OH^– + 3H₂O + 3Cl₂ → 5Cl­^– + ClO₃­^– + 6H₂O

Removing excess of water

6OH^– + 3H₂O + 3Cl₂ → 5Cl­^– + ClO₃­^– + 6H₂O

6OH^– + 3Cl₂ → 5Cl­^– + ClO₃­^– + 3H₂O

Answer: 6OH^– + 3Cl₂ → 5Cl­^– + ClO₃­^– + 3H₂O

Atom	Number in reactants	Number in products
Cl	6	6
H	6	6
O	6	6
Charges	6	6

Back to list of exercises

---

10. Balance in acidic conditions MnO₄^–(aq) + H₂C₂O₄(aq) → Mn²⁺(aq) + CO₂(g)

Answer: 2MnO₄^–(aq) + 5H₂C₂O₄(aq) + 6H⁺(aq)→ 2Mn²⁺(aq)+ 8H₂O(l) + 10CO₂(g)

Half reactions:

Reduction:          MnO₄^– → Mn²⁺

Oxidation:           H₂C₂O₄ → CO₂

Adjusting elements except for O and H:

Reduction:          MnO₄^– → Mn²⁺

Oxidation:           H₂C₂O₄ → 2CO₂

Adjusting O by adding H₂O:

Reduction:          MnO₄^– → Mn²⁺ + 4H₂O

Oxidation:           H₂C₂O₄ → 2CO₂

Adjusting H by adding H⁺:

Reduction:          8H⁺ + MnO₄^– → Mn²⁺ + 4H₂O

Oxidation:           H₂C₂O₄ → 2CO₂ + 2H⁺

Equalizing charges by adding e^–:

Reduction:          5e^– + 8H⁺ + MnO₄^– → Mn²⁺ + 4H₂O

Oxidation:           H₂C₂O₄ → 2CO₂ + 2H⁺ + 2e^–

Equalizing electrons in both half-equations:

Reduction:          2 x (5e^– + 8H⁺ + MnO₄^– → Mn²⁺ + 4H₂O)

10e^– + 16H⁺ + 2MnO₄^– → 2Mn²⁺ + 8H₂O

Oxidation:           5 x (H₂C₂O₄ → 2CO₂ + 2 H⁺ + 2e^–)

5H₂C₂O₄ → 10CO₂ + 10H⁺ + 10e^–

Adding both half-equations:

Reduction:  10e^– + 16H⁺ + 2MnO₄^– → 2Mn²⁺ + 8H₂O

Oxidation:  5H₂C₂O₄ → 10CO₂ + 10H⁺ + 10e^–

————————————————————————-

Full equation:  10e^– + 16H⁺ + 2MnO₄^– + 5H₂C₂O₄ → 2Mn²⁺ + 8H₂O + 10CO₂^– + 10H⁺ + 10e^–

Cancelling electrons common terms:

10e^– + 16H⁺ + 2MnO₄^– + 5H₂C₂O₄ → 2Mn²⁺ + 8H₂O + 10CO₂ + 10H⁺ + 10e^–

6H⁺ + 2MnO₄^– + 5H₂C₂O₄ → 2Mn²⁺ + 8H₂O + 10CO₂^–

Result

2MnO₄^–(aq) + 5H₂C₂O₄(aq) + 6H⁺(aq) → 2Mn²⁺(aq) + 8H₂O(aq) + 10CO₂(g)

Atom	Number in reactants	Number in products
Mn	2	2
O	28	28
C	10	10
H	16	16
Charges	4+	4+

Back to list of exercises

---

11. Balance in acidic conditions Cr₂O₇^2-(aq) + Fe²⁺(aq) → Cr³⁺(aq) + Fe³⁺(aq)

Answer: Cr₂O₇^2-(aq) + 6Fe²⁺(aq) + 14H⁺(aq) → 2Cr³⁺(aq) + 6Fe³⁺(aq) + 7H₂O(l)

 

Half reactions:

Reduction:          Cr₂O₇^2- → Cr³⁺

Oxidation:           Fe²⁺ → Fe³⁺

Adjusting elements except for O and H:

Reduction:          Cr₂O₇^2- → 2Cr³⁺

Oxidation:           Fe²⁺ → Fe³⁺

Adjusting O by adding H₂O:

Reduction:          Cr₂O₇^2- → 2Cr³⁺ + 7H₂O

Oxidation:           Fe²⁺ → Fe³⁺

Adjusting H by adding H⁺:

Reduction:          14H⁺ + Cr₂O₇^2- → 2Cr³⁺ + 7H₂O

Oxidation:           Fe²⁺ → Fe³⁺

Equalizing charges by adding e^–:

Reduction:          6e^– + 14H⁺ + Cr₂O₇^2- → 2Cr³⁺ + 7H₂O

Oxidation:           Fe²⁺ → Fe³⁺ + e^–

Equalizing electrons in both half-equations:

Reduction:          6e^– + 14H⁺ + Cr₂O₇^2- → 2Cr³⁺ + 7H₂O

Oxidation:           6 x (Fe²⁺ → Fe³⁺ + e^–)

6Fe²⁺ → 6Fe³⁺ + 6e^–

Adding both half-equations:

Reduction:  6e^– + 14H⁺ + Cr₂O₇^2- → 2Cr³⁺ + 7H₂O

Oxidation:  6Fe²⁺ → 6Fe³⁺ + 6e^–

—————————————————————–

Full equation:  :  6e^– + 14H⁺ + Cr₂O₇^2- + 6Fe²⁺ → 2Cr³⁺ + 7H₂O + 6Fe³⁺ + 6e^–

Cancelling electrons common terms:

6e^– + 14H⁺ + Cr₂O₇^2- + 6Fe²⁺ → 2Cr³⁺ + 7H₂O + 6Fe³⁺ + 6e^–

14H⁺ + Cr₂O₇^2- + 6Fe²⁺ → 2Cr³⁺ + 7H₂O + 6Fe³⁺

Result

Cr₂O₇^2-(aq) + 6Fe²⁺(aq) + 14H⁺(aq) → 2Cr³⁺(aq) + 6Fe³⁺(aq) + 7H₂O(l)

Atom	Number in reactants	Number in products
Cr	2	2
O	7	7
Fe	6	6
H	14	14
Charges	24+	24+

Back to list of exercises

12. Balance in acidic conditions MnO₄^–(aq) + H₂SO₃(aq) → Mn²⁺(aq) + SO₄^2-(aq)

Answer: 2MnO₄^–(aq) + 5H₂SO₃(aq) → 2Mn²⁺(aq) + 5SO₄^2-(aq) + 3H₂O(l) + 4H⁺(aq)

Half reactions:

Reduction:          MnO₄^– → Mn²⁺

Oxidation:           H₂SO₃ → SO₄^2-

Adjusting elements except for O and H (no change):

Reduction:          MnO₄^– → Mn²⁺

Oxidation:           H₂SO₃ → SO₄^2-

Adjusting O by adding H₂O:

Reduction:          MnO₄^– → Mn²⁺ + 4H₂O

Oxidation:           H₂O + H₂SO₃ → SO₄^2-

Adjusting H by adding H⁺:

Reduction:          8H⁺ + MnO₄^– → Mn²⁺ + 4H₂O

Oxidation:           H₂O + H₂SO₃ → SO₄^2- + 4H⁺

Equalizing charges by adding e^–:

Reduction:          5e^– + 8H⁺ + MnO₄^– → Mn²⁺ + 4H₂O

Oxidation:           H₂O + H₂SO₃ → SO₄^2- + 4H⁺ + 2e^–

Equalizing electrons in both half-equations:

Reduction:          2 x (5e^– + 8H⁺ + MnO₄^– → Mn²⁺ + 4H₂O)

10e^– + 16H⁺ + 2MnO₄^– → 2Mn²⁺ + 8H₂O

Oxidation:           5 x (H₂O + H₂SO₃ → SO₄^2- + 4H⁺ + 2e^–)

5H₂O + 5H₂SO₃ → 5SO₄^2- + 20H⁺ + 10e^–

Adding both half-equations:

Reduction:  10e^– + 16H⁺ + 2MnO₄^– → 2Mn²⁺ + 8H₂O

Oxidation:  5H₂O + 5H₂SO₃ → 5SO₄^2- + 20H⁺ + 10e^–

———————————————————————————-

Full equation:  10e^– + 16H⁺ + 2MnO₄^– + 5H₂O + 5H₂SO₃ → 2Mn²⁺ + 8H₂O + 5SO₄^2- + 20H⁺ + 10e^–

Cancelling electrons common terms:

10e^– + 16H⁺ + 2MnO₄^– + 5H₂O + 5H₂SO₃ → 2Mn²⁺ + 8H₂O + 5SO₄^2- + 20H⁺ + 10e-

2MnO₄^– + 5H₂SO₃ → 2Mn²⁺ + 3H₂O + 5SO₄^2- + 4H⁺

Result

2MnO₄^–(aq) + 5H₂SO₃(aq) → 2Mn²⁺(aq) + 5SO₄^2-(aq) + 3H₂O(l) + 4H⁺(aq)

Atom	Number in reactants	Number in products
Mn	2	2
O	23	23
H	10	10
S	5	5
Charges	2-	2-

Back to list of exercises

---

13. Balance in basic conditions MnO₄^–(aq) + SO₃^2-(aq) → MnO₂(s) + SO₄^2-(aq)

Answer: 2MnO₄^–(aq) + 3SO₃^2-(aq) + H₂O(l) → 2MnO₂(s) + 3SO₄^2-(aq) + 2OH^–(aq)

Half reactions:

Reduction:          MnO₄^– → MnO₂

Oxidation:           SO₃^2- → SO₄^2-

Adjusting elements except for O and H (no change):

Reduction:          MnO₄^– → MnO₂

Oxidation:           SO₃^2- → SO₄^2-

Adjusting O by adding H₂O:

Reduction:          MnO₄^– → MnO₂ + 2H₂O

Oxidation:           H₂O + SO₃^2- → SO₄^2-

Adjusting H by adding H⁺:

Reduction:          4H⁺ + MnO₄^– → MnO₂ + 2H₂O

Oxidation:           H₂O + SO₃^2- → SO₄^2- + 2H⁺

Equalizing charges by adding e^–:

Reduction:          3e^– + 4H⁺ + MnO₄^– → MnO₂ + 2H₂O

Oxidation:           H₂O + SO₃^2- → SO₄^2- + 2H⁺ + 2e^–

Equalizing electrons in both half-equations:

Reduction:          2 x (3e^– + 4H⁺ + MnO₄^– → MnO₂ + 2H₂O)

6e^– + 8H⁺ + 2MnO₄^– → 2MnO₂ + 4H₂O

Oxidation:           3 x (H₂O + SO₃^2- → SO₄^2- + 2H⁺ + 2e^–)

3H₂O + 3SO₃^2- → 3SO₄^2- + 6H⁺ + 6e^–

Adding both half-equations:

Reduction: 6e^– + 8H⁺ + 2MnO₄^– → 2MnO₂ + 4H₂O

Oxidation:  3H₂O + 3SO₃^2- → 3SO₄^2- + 6H⁺ + 6e^–

———————————————————————————-

Full equation:  6e^– + 8H⁺ + 2MnO₄^– + 3H₂O + 3SO₃^2- → 2MnO₂ + 4H₂O + 3SO₄^2- + 6H⁺ + 6e^–

Cancelling electrons common terms:

6e^– + 8H⁺ + 2MnO₄^– + 3H₂O + 3SO₃^2- → 2MnO₂ + 4H₂O + 3SO₄^2- + 6H⁺ + 6e-

2H⁺ + 2MnO₄^– + 3SO₃^2- → 2MnO₂ + H₂O + 3SO₄^2-

Adding OH^– in each side of the equation as H⁺ we have:

2OH^– + 2H⁺ + 2MnO₄^– + 3SO₃^2- → 2MnO₂ + H₂O + 3SO₄^2- + 2OH^–

Forming H₂O from H⁺ and OH^–:

2H₂O + 2MnO₄^– + 3SO₃^2- → 2MnO₂ + H₂O + 3SO₄^2- + 2OH^–

Removing excess of water

2H₂O + 2MnO₄^– + 3SO₃^2- → 2MnO₂ + H₂O + 3SO₄^2- + 2OH^–

H₂O + 2MnO₄^– + 3SO₃^2- → 2MnO₂ + 3SO₄^2- + 2OH^–

Result:

2MnO₄^–(aq) + 3SO₃^2-(aq) + H₂O(l) → 2MnO₂(s) + 3SO₄^2-(aq) + 2OH^–(aq)

Atom	Number in reactants	Number in products
Mn	2	2
O	18	18
H	2	2
S	3	3
Charges	8-	8-

Back to list of exercises

---

14. Balance in basic conditions MnO₄^–(aq) + Br^–(aq) → MnO₂(s) + BrO₃^–(aq)

Answer: 2MnO₄^–(aq) + Br^–(aq) + H₂O(l) → 2MnO₂(s) + BrO₃^–(aq) + 2OH^–(aq)

Half reactions:

Reduction:          MnO₄^– → MnO₂

Oxidation:           Br^-‑→ BrO₃^–

Adjusting elements except for O and H (no change):

Reduction:          MnO₄^– → MnO₂

Oxidation:           Br^–→ BrO₃^–

Adjusting O by adding H₂O:

Reduction:          MnO₄^– → MnO₂ + 2H₂O

Oxidation:           3H₂O + Br^–→ BrO₃^–

Adjusting H by adding H⁺:

Reduction:          4H⁺ + MnO₄^– → MnO₂ + 2H₂O

Oxidation:           3H₂O + Br^‑→ BrO₃^–+ 6H⁺

Equalizing charges by adding e^–:

Reduction:          3e^– + 4H⁺ + MnO₄^– → MnO₂ + 2H₂O

Oxidation:           3H₂O + Br^‑→ BrO₃^–+ 6H⁺ + 6e^–

Equalizing electrons in both half-equations:

Reduction:          2 x (3e^– + 4H⁺ + MnO₄^– → MnO₂ + 2H₂O)

6e^– + 8H⁺ + 2MnO₄^– → 2MnO₂ + 4H₂O

Oxidation:           3H₂O + Br^‑→ BrO₃^–+ 6H⁺ + 6e^–

Adding both half-equations:

Reduction: 6e^– + 8H⁺ + 2MnO₄^– → 2MnO₂ + 4H₂O

Oxidation:  3H₂O + Br^‑ → BrO₃^–+ 6H⁺ + 6e^–

———————————————————————————-

Full equation:  6e^– + 8H⁺ + 2MnO₄^– + 3H₂O + Br^‑ → 2MnO₂ + 4H₂O + BrO₃^– + 6H⁺ + 6e^–

Cancelling electrons common terms:

6e^– + 8H⁺ + 2MnO₄^– + 3H₂O + Br^‑ → 2MnO₂ + 4H₂O + BrO₃^– + 6H⁺ + 6e-

2H⁺ + 2MnO₄^– + Br^– → 2MnO₂ + H₂O + BrO₃^–

Adding OH^– in each side of the equation as H⁺ we have:

2OH^– + 2H⁺ + 2MnO₄^– + Br^– → 2MnO₂ + H₂O + BrO₃^– + 2OH^–

Forming H₂O from H⁺ and OH^–:

2H₂O + 2MnO₄^– + Br^– → 2MnO₂ + H₂O + BrO₃^– + 2OH^–

Removing excess of water

2H₂O + 2MnO₄^– + Br^– → 2MnO₂ + H₂O + BrO₃^2- + 2OH^–

H₂O + 2MnO₄^– + Br^– → 2MnO₂ + BrO₃^– + 2OH^–

Result:

2MnO₄^–(aq) + Br^–(aq) + H₂O(l) → 2MnO₂(s) + BrO₃^–(aq) + 2OH^–(aq)

Atom	Number in reactants	Number in products
Mn	2	2
O	9	9
H	2	2
Br	1	1
Charges	3-	3-

Back to list of exercises

---

15. Balance in acidic conditions Cu(s) + NO₃^–(aq) → Cu²⁺(aq) + NO(g)

Answer: 3Cu(aq) + 2NO₃^–(aq) + 8H⁺(aq) → 3Cu²⁺(aq) + 2NO(g) + 4H₂O(l)

Half reactions:

Reduction:          NO₃^– → NO

Oxidation:           Cu → Cu²⁺

Adjusting elements except for O and H (no change):

Reduction:          NO₃^– → NO

Oxidation:           Cu → Cu²⁺

Adjusting O by adding H₂O:

Reduction:          NO₃^– → NO + 2H₂O

Oxidation:           Cu → Cu²⁺

Adjusting H by adding H⁺:

Reduction:          4H⁺ + NO₃^– → NO + 2H₂O

Oxidation:           Cu → Cu²⁺

Equalizing charges by adding e^–:

Reduction:          3e^– + 4H⁺ + NO₃^– → NO + 2H₂O

Oxidation:           Cu → Cu²⁺ + 2e^–

Equalizing electrons in both half-equations:

Reduction:          2 x (3e^– + 4H⁺ + NO₃^– → NO + 2H₂O)

6e^– + 8H⁺ + 2NO₃^– → 2NO + 4H₂O

Oxidation:           3 x (Cu → Cu²⁺ + 2e^–)

3Cu → 3Cu²⁺ + 6e^–

Adding both half-equations:

Reduction:  6e^– + 8H⁺ + 2NO₃^– → 2NO + 4H₂O

Oxidation:  3Cu → 3Cu²⁺ + 6e^–

———————————————————————————-

Full equation:  6e^– + 8H⁺ + 2NO₃^– + 3Cu → 2NO + 4H₂O + 3Cu²⁺ + 6e^–

Cancelling electrons common terms:

6e^– + 8H⁺ + 2NO₃^– + 3Cu → 2NO + 4H₂O + 3Cu²⁺ + 6e-

8H⁺ + 2NO₃^– + 3Cu → 2NO + 4H₂O + 3Cu²⁺

Result

3Cu(aq) + 2NO₃^–(aq) + 8H⁺(aq) → 3Cu²⁺(aq) + 2NO(g) + 4H₂O(l)

Atom	Number in reactants	Number in products
Cu	3	3
N	2	2
O	6	6
H	8	8
Charges	6+	6+

Back to list of exercises

---

16. Balance in acidic conditions: SO₄^2-(aq) + Zn(s) → H₂S(g) + Zn²⁺(aq)

Answer: SO₄^2–(aq) + 4Zn(s) + 10H⁺(aq) → H₂S(g) + 4Zn²⁺(aq) + 4H₂O(l)

Half reactions:

Reduction:          SO₄^2- → H₂S

Oxidation:           Zn → Zn²⁺

Adjusting elements except for O and H (no change):

Reduction:          SO₄^2- → H₂S

Oxidation:           Zn

Adjusting O by adding H₂O:

Reduction:          SO₄^2- → H₂S + 4H₂O

Oxidation:           Zn → Zn²⁺

Adjusting H by adding H⁺:

Reduction:          SO₄^2- + 10H⁺ → H₂S + 4H₂O

Oxidation:           Zn → Zn²⁺

Equalizing charges by adding e^–:

Reduction:          SO₄^2- + 10H⁺ + 8e^–→ H₂S + 4H₂O

Oxidation:           Zn → Zn²⁺ + 2e^–

Equalizing electrons in both half-equations:

Reduction:          SO₄^2- + 10H⁺ + 8e^–→ H₂S + 4H₂O

Oxidation:           4 x (Zn → Zn²⁺ + 2e^–)

4Zn → 4Zn²⁺ + 8e^–

Adding both half-equations:

Reduction:          SO₄^2- + 10H⁺ + 8e^–→ H₂S + 4H₂O

Oxidation:           4Zn → 4Zn²⁺ + 8e^–

———————————————————————————-

Full equation:  SO₄^2- + 10H⁺ + 8e^– + 4Zn → H₂S + 4H₂O + 4Zn²⁺ + 8e^–

Cancelling electrons and common terms and adding physical states:

SO₄^2- + 10H⁺ + 8e^– + 4Zn → H₂S + 4H₂O + 4Zn²⁺ + 8e^–

Result (with indication of the physical states)

SO₄^2–(aq) + 4Zn(s) + 10H⁺(aq) → H₂S(g) + 4Zn²⁺(aq) + 4H₂O(l)

Atom	Number in reactants	Number in products
S	1	1
O	4	4
Zn	4	4
H	10	10
Charges	8+	8+

Back to list of exercises

---

17. Balance in acidic conditions: SO₄^2-(aq) + Cu(s) → SO₂(g) + Cu²⁺(aq)

Answer: SO₄^2–(aq) + Cu(s) + 4H⁺(aq) → SO₂(g) + Cu²⁺(aq) + 2H₂O(l)

Half reactions:

Reduction:          SO₄^2- → SO₂

Oxidation:           Cu → Cu²⁺

Adjusting elements except for O and H (no change):

Reduction:          SO₄^2- → SO₂

Oxidation:           Cu → Cu²⁺

Adjusting O by adding H₂O:

Reduction:          SO₄^2- → SO₂ + 2H₂O

Oxidation:           Cu → Cu²⁺

Adjusting H by adding H⁺:

Reduction:          SO₄^2- + 4H⁺→ SO₂ + 2H₂O

Oxidation:           Cu → Cu²⁺

Equalizing charges by adding e^–:

Reduction:          SO₄^2- + 4H⁺+ 2e^–→ SO₂ + 2H₂O

Oxidation:           Cu → Cu²⁺+ 2e^–

Equalizing electrons in both half-equations (no change):

Reduction:          SO₄^2- + 4H⁺+ 2e^–→ SO₂ + 2H₂O

Oxidation:           Cu → Cu²⁺+ 2e^–

Adding both half-equations:

Reduction:          SO₄^2- + 4H⁺+ 2e^–→ SO₂ + 2H₂O

Oxidation:           Cu → Cu²⁺+ 2e^–

———————————————————————————-

Full equation:  SO₄^2- + 4H⁺ + 2e^– + Cu → SO₂ +2H₂O + + Cu²⁺ + 2e^–

Cancelling electrons and common terms:

SO₄^2- + 4H⁺ + 2e^– + Cu → SO₂ +2H₂O + + Cu²⁺ + 2e^–

Result (with indication of the physical states)

SO₄^2–(aq) + Cu(s) + 4H⁺(aq) → SO₂(g) + Cu²⁺(aq) + 2H₂O(l)

Atom	Number in reactants	Number in products
S	1	1
O	4	4
Cu	1	1
H	4	4
Charges	2+	2+

Back to list of exercises

---

Comments

If you have any question, or want to add anything else, please leave a comment below. Also, if you have a chemical equation difficult you can post it below, we can try to solve it.