If you find this useful, please leave a comment at the end of the page.

SECTION B
16
This question is about energy changes.
(a)
Lattice enthalpies can be determined indirectly using Born-Haber cycles.
The table below shows the energy changes that are needed to determine the lattice enthalpy of barium iodide, BaI2.
| Energy term | Energy change/kJmol–1 |
| Formation of barium iodide | –602 |
| 1st electron affinity of iodine | –296 |
| 1st ionisation energy of barium | +503 |
| 2nd ionisation energy of barium | +965 |
| Atomisation of iodine | +107 |
| Atomisation of barium | +180 |
(i)
The diagram below shows an incomplete Born-Haber cycle that can be used to calculate the lattice enthalpy of barium iodide.
On the dotted lines, add the species present, including state symbols.
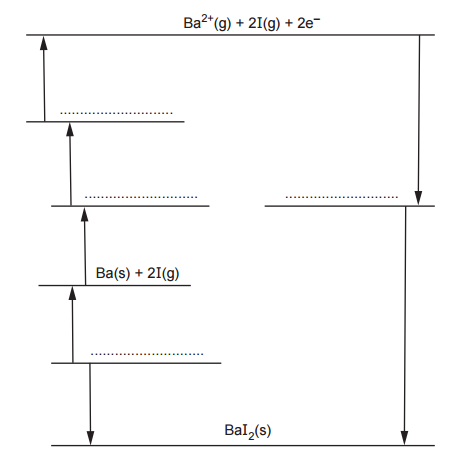
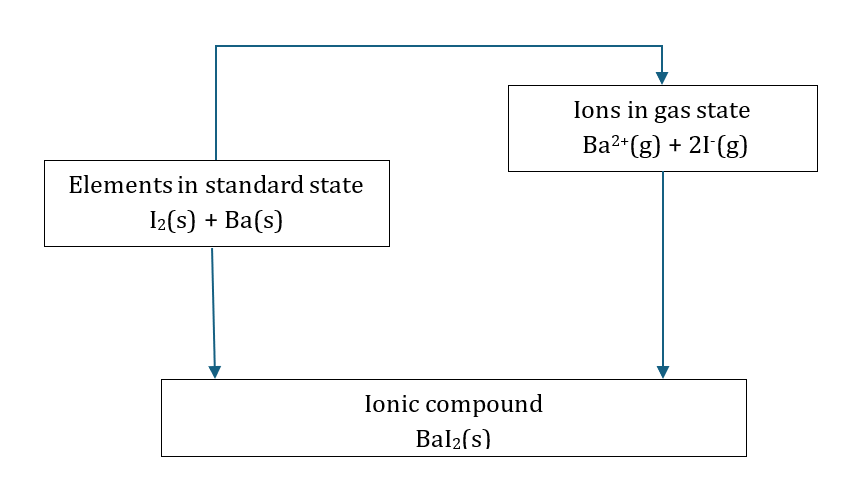
In a Born-Haber cycle, there are always 3 related elements:
- The elements in standard state: I2(s) and Ba(s)
- The ions in gas state: Ba2+(g) and I–(g)
- The ionic compound: BaI2(s)
We can sketch the following diagram:
To complete the diagram, we need to fill the gaps with the relevant energies following the criteria that:
- In exothermic reactions (ΔH<0) the energy goes down.
- In endothermic reactions (ΔH>0) the energy goes up.
To help to solve this problem, I expand the table with the different reactions.
| Energy term | Energy change/kJmol–1 | Reaction |
| Formation of barium iodide | –602 | Ba (s) +I2(s) → BaI2(s) |
| 1st electron affinity of iodine | –296 | I (g) + e− → I−(g) |
| 1st ionisation energy of barium | +503 | Ba (g) → Ba+(g) + e− |
| 2nd ionisation energy of barium | +965 | Ba+(g) → Ba2+(g) + e− |
| Atomisation of iodine | +107 | ½ I2(s) → I (g) |
| Atomisation of barium | +180 | Ba(s)→Ba(g) |
Using this information, we can complete the given diagram. I have highlighted the equations from the table above and the energy changes in red, as we will use these energy changes in the next question. Note that I have multiplied the first electron affinity of iodine and the atomisation of iodine by 2, since we are using twice the quantities indicated in the equations. The results for this question are shown in blue. Additionally, I have included the results from the marking scheme for clarity.
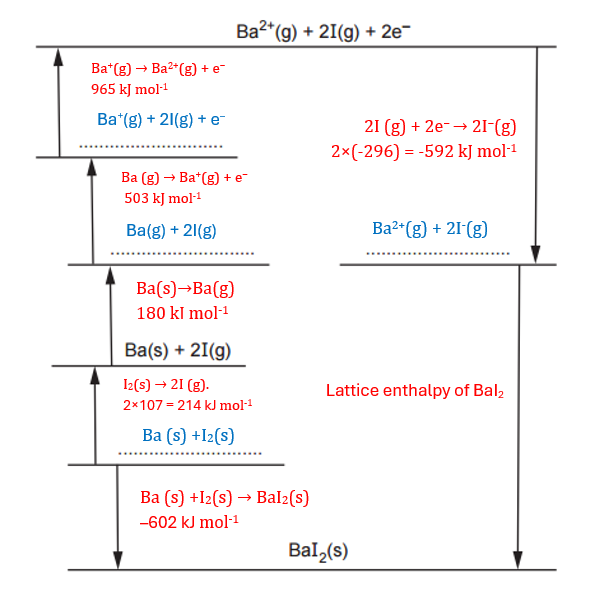
From the marking scheme:

(ii)
Calculate the lattice enthalpy of barium iodide.
Using the diagram and Hess’s Law—which states that ‘the total energy change of a chemical reaction is the same, regardless of the pathway or sequence of steps, as long as the initial and final states are identical‘—we can determine that the energy for the reaction via ‘Route 1’ should be the same as that via ‘Route 2’.
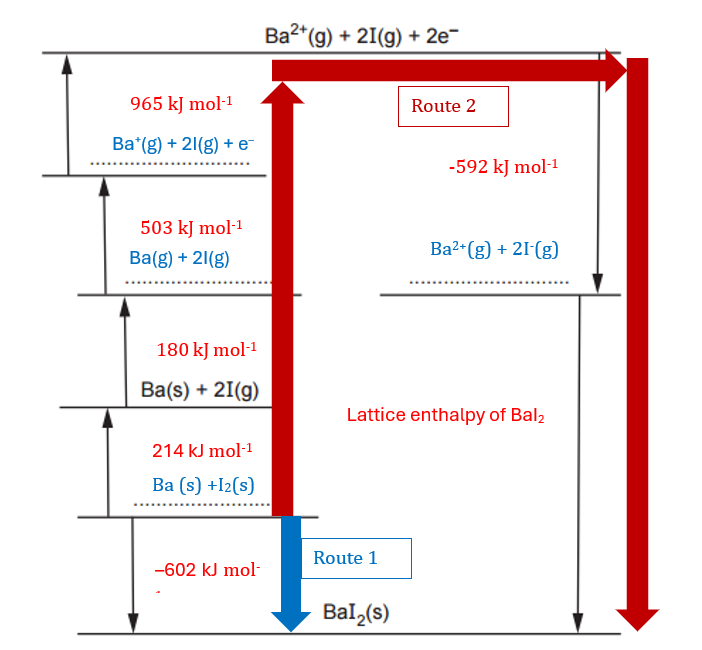
We have the following calculation:
−602=214+180+503+965+(−592)+Lattice enthalpy
Simplifying:
-602 = 1270 + Lattice enthalpy
Solving for the lattice enthalpy:
Lattice enthalpy = -602 – 1270 = -1872
Note: Be cautious with the signs, as it’s easy to mistakenly use a positive sign here, which would cost 1 mark. Remember that lattice enthalpy represents an exothermic reaction, meaning the energy change is negative.
lattice enthalpy = ……………………-1872……………….. kJ mol–1
[2]
(b)
The first and second ionisation energies of magnesium, Mg, and strontium, Sr, in Group 2 are given in the table below.
| Element | First ionisation energy /kJ mol-1 | Second ionisation energy /kJ mol-1 |
|---|---|---|
| Mg | +738 | +1451 |
| Sr | +550 | +1064 |
- Explain why the first ionisation energy of Mg is greater than the first ionisation energy of Sr.
- Explain why the second ionisation energy of Sr is greater than the first ionisation energy of Sr.
Ionisation energy is the amount of energy required to remove one mole of electrons from one mole of gaseous atoms or ions to form positively charged ions. For example, for Mg:
Mg(g) → Mg+(g) + 1e–
Therefore, ionisation energy is related to the strength of the attraction between an electron and the nucleus of an atom or ion.
Magnesium has a higher first ionisation energy than strontium because its smaller atomic size and reduced shielding result in a stronger nuclear attraction to the outermost electron, making it harder to remove.
Strontium’s second ionisation energy is greater than its first because, after the first electron is removed, the remaining electrons experience a stronger effective nuclear charge and are closer to the nucleus, requiring more energy to remove.
17*
Bromine, Br2, can be produced by the reaction:
5Br–(aq) + BrO3–(aq) + 6H+(aq) → 3Br2(aq) + 3H2O(l)
A student investigates the rate of this reaction by carrying out four experiments at the same temperature. The student’s results are shown below.
| Experiment | [Br –] /mol dm–3 | [BrO3–] /mol dm–3 | [H+] /mol dm–3 | Initial rate /mol dm–3 s–1 |
|---|---|---|---|---|
| 1 | 2.00 × 10–2 | 1.20 × 10–1 | 8.00 × 10–2 | 2.52 × 10–4 |
| 2 | 6.00 × 10–2 | 1.20 × 10–1 | 8.00 × 10–2 | 7.56 × 10–4 |
| 3 | 4.00 × 10–2 | 6.00 × 10–2 | 8.00 × 10–2 | 2.52 × 10–4 |
| 3 | 2.00 × 10–2 | 6.00 × 10–2 | 4.00 × 10–1 | 3.15 × 10–3 |
Explain how the reaction orders can be determined from the student’s results, and determine the rate equation and rate constant for this reaction.
To measure reaction rates, we change the concentration of one reactant while keeping the others constant. This helps isolate the effect of that specific reactant. What we are looking for is:
- If doubling the concentration of a reactant doubles the rate, the reaction is first order with respect to that reactant (m = 1).
- If doubling the concentration causes the rate to quadruple, the reaction is second order (m = 2)
- If changing the concentration doesn’t affect the rate, the reaction is zero order (m = 0).
Often, a quick visual comparison of the numbers helps identify the correct values. However, if the pattern isn’t immediately obvious, a more systematic and numerical approach helps. I will explain here in both ways.
The rate equation for this reaction can be expressed as:
Rate = k [Br–]a [BrO3–]b [H+]c
Where k is the rate constant and a, b, and c are the reaction orders for Br–, BrO3– and H+ respectively. To solve the problem, we select experiments where we can simplify some of the terms in the rate equation and calculate the relevant reaction orders.
By comparing experiment 1 and experiment 2, we see that in experiment 2, the student has trebled the concentration of Br⁻, while keeping BrO₃⁻ and H⁺ constant. The initial rate also trebles, which suggests that the reaction rate is directly proportional to [Br⁻]. This means the reaction order with respect to Br⁻ is 1 (a = 1). Or using a more systematic approach, if we divide the results from experiment 2 by those from experiment 1:
$$
\small{\frac{\text{Experiment 2}}{\text{Experiment 1}}:}
\frac{7.56 \times 10^{-4}}{2.52 \times 10^{-4}} =
\frac{k (6.00 \times 10^{-2})^a (1.20 \times 10^{-1})^b (8.00 \times 10^{-2})^c}
{k (2.00 \times 10^{-2})^a (1.20 \times 10^{-1})^b (8.00 \times 10^{-2})^c}
$$
Operating and simplifying, we get:
$$
\small{\frac{7.56 \times 10^{-4}}{2.52 \times 10^{-4}} =
\frac{(6.00 \times 10^{-2})^a}{(2.00 \times 10^{-2})^a}}
$$
3 = 3a
Meaning that a = 1.
If we compare experiment 1 with experiment 3, we notice that in experiment 3, the initial concentration of Br⁻ has been doubled, while the concentration of BrO₃⁻ has been halved. Despite these changes, the initial rate of reaction remains the same. Since we already know that the reaction order with respect to Br⁻ is 1 (a = 1), we can conclude that the reaction order for BrO₃⁻ is also 1 (b = 1). Alternatively, we could confirm this using a more systematic method:
$$
\small{\frac{\text{Experiment 3}}{\text{Experiment 1}}:
\frac{2.52 \times 10^{-4}}{2.52 \times 10^{-4}} =
\frac{k (4.00 \times 10^{-2})^1 (6.00 \times 10^{-2})^b (8.00 \times 10^{-2})^c}
{k (2.00 \times 10^{-2})^1 (1.20 \times 10^{-1})^b (8.00 \times 10^{-2})^c}
}
$$
Simplifying:
$$
\small{1 = \frac{4.00 \times 10^{-2}}{2.00 \times 10^{-2}} \left( \frac{6.00 \times 10^{-2}}{1.20 \times 10^{-1}} \right)^b}
$$
1 = 2 × 0.5b
0.5 = 0.5b
This means that b = 1
The only reaction order left is c. The initial concentration of H+ has only changed in experiment 4. Using the information that we have (including a = b = 1), experiment 3 and experiment 4:
$$\small
\frac{\text{Experiment 3}}{\text{Experiment 4}}:
\frac{2.52 \times 10^{-4}}{3.15 \times 10^{-3}} =
\frac{k \, (4.00 \times 10^{-2})^1 \, (6.00 \times 10^{-2})^1 \, (8.00 \times 10^{-2})^c}{k \, (2.00 \times 10^{-2})^1 \, (6.00 \times 10^{-2})^1 \, (4.00 \times 10^{-1})^c}
$$
Simplifying:
$$\small
0.08 = 2 \times \left(\frac{8.00 \times 10^{-2}}{4.00 \times 10^{-1}}\right)^c
$$
0.08 = 2 × 0.2c
0.04 = 0.2c
Taking logarithms:
log (0.04) = c log (0.2)
c = log (0.04) / log (0.2) = 2
Then, c = 2
With the reaction orders, we can calculate the reaction constant by using the data from any of the experiments. Taking experiment 1:
Rate = k [Br–]1 [BrO3–]1 [H+]2
2.52×10-4 = k (2.00×10-2) (1.20×10-1) (8.00×10-2)2
$$\small
k = \frac{2.52 \times 10^{-4}}{0.02 \times 0.12 \times (0.08)^2} = 16.40625
$$
To calculate the units of k, we use the rate equation, making k the subject and replacing the relevant units:
$$\small
k = \frac{\text{Rate}}{[ \text{Br}^-]^1 [ \text{BrO}_3^-]^1 [ \text{H}^+]^2} =
\frac{\text{mol} \, \text{dm}^{-3} \, \text{s}^{-1}}{(\text{mol} \, \text{dm}^{-3})^1 (\text{mol} \, \text{dm}^{-3})^1 (\text{mol} \, \text{dm}^{-3})^2} = \text{mol}^{-3} \, \text{dm}^9 \, \text{s}^{-1}
$$
Then, k = 16.4 mol-3 dm9 s-1
[6]
18
This question is about enthalpy changes of reactions involving hydrocarbons.
(a)
A student determines the enthalpy change of combustion, ∆cH, of heptane, C7H16, using the method outlined below.
- Add 150g of water to a beaker and measure its temperature.
- Weigh a spirit burner containing heptane and use it to heat the water.
- Extinguish the flame and record the maximum temperature reached by the water.
- Reweigh the spirit burner.
The temperature of the water increased by 10.5°C.
The spirit burner decreased in mass by 0.133g.
Use the student’s results to determine the enthalpy change of combustion of heptane, ∆cH (C7H16), in kJmol–1.
The temperature increase in the experiment is due to the heat released during the combustion of heptane. Assuming there are no heat losses, the heat energy can be calculated using the formula:
q = mcΔT
Using the specific heat capacity of water given in the data sheet (4.18 J/g°C) and the experimental data provided, we calculate:
q = 150 × 4.18 × 10.5 = 6,583.5 J
q = 6.5835 kJ
This heat energy corresponds to the combustion of 0.133 g of heptane. With the molecular mass of heptane calculated as:
(7 × 12) + (16 × 1) = 100 g/mol
The enthalpy change of combustion for heptane can be found as:
$$
{\small \frac{6.5835 \, \text{kJ}}{0.133 \, \text{g Heptane}} \times \frac{100 \, \text{g Heptane}}{1 \, \text{mol Heptane}} = 4950 \, \text{kJ mol}^{-1}}
$$
We have to change the sign to negative, as combustion is an exothermic reaction.
∆cH (C7H16) = …………………………………-4,950…. kJmol–1
[3]
(b)
Nonane, C9H20, can be broken down by heat to form pentane, C5H12, and ethene, C2H4.
C9H20(g) → C5H12(g) + 2C2H4(g)
∆H = +186kJmol–1
Reaction 1
The enthalpy changes of combustion of C9H20(g) and C2H4(g) are shown in the table below.
| Hydrocarbon | ∆cH/kJmol–1 |
|---|---|
| C9H20(g) | –6171 |
| C2H4(g) | –1411 |
Use ∆H in Reaction 1 and the enthalpy changes of combustion in the table to determine the enthalpy change of combustion of C5H12(g)
To solve the problem, we can use:
ΔH (reaction) = Σ ΔcH (reactants) – Σ ΔcH (products)
Alternatively, we can use Hess’s law, which states that the total enthalpy change of a chemical reaction is independent of the path taken, as long as the initial and final states remain the same. Both approaches effectively lead to the same solution, as it is the same approach:
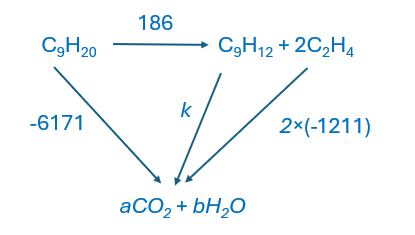
Using the equation:
ΔH (reaction) = Σ ΔcH (reactants) – Σ ΔcH (products)
We can replace the values obtained and solve the equation:
ΔH = (ΔcHC9H20) – (ΔcHC5H12 + 2× ΔcHC2H4)
186 = (-6171) – [ΔcHC5H12 + 2× (-1411)]
186 = -6171 – (ΔcHC5H12 – 2822)
186 = -6171 – ΔcHC5H12 + 2822
186 = -3349 – ΔcHC5H12
-ΔcHC5H12 = 186 + 3349 = 3535
ΔcHC5H12 = – 3535 kJ/mol
To use Hess’s law. I number the reactions as ‘Equations’ to avoid confusion with the names used on the paper. The 1st equation is ‘Reaction 1’
Equation 1: C9H20(g) → C5H12(g) + 2C2H4(g) ΔH = +186 kJ/mol
Now we write the enthalpy change of combustion for nonane and ethene (remember that these needs to be balanced)
Equation 2: C9H20(g) + 14O2 → 10H2O(l) + 9CO2(g) ΔH = -6171 kJ/mol
Equation 3: C2H4(g) + 3O2 → 2H2O(l) + 2CO2(g) ΔH = -1411 kJ/mol
And finally, the reaction that we are looking for: the enthalpy change of combustion for pentane:
Equation 4: C5H12(g) + 8 O2 → 6H2O(l) + 5CO2(g) ΔH = ? kJ/mol
In the next steps, we arrange equations 1 to 3 to obtain equation 4. To make things easier to follow, I go step by step, if you are familiar with this type of problems, you can put all the steps together in 1 go.
Step 1: Reverse Equation 1 to get pentane on the reactant side (change the sign of ΔH):
I call this Equation 1a
Equation 1a: C5H12(g) + 2C2H4(g) → C9H20(g) ΔH = -186 kJ/mol
Step 2. Eliminate C9H20(g) using Equation 2
Adding equations 2 and 1a, we get Equation 1b:
Equation 1a:
C5H12(g) + 2C2H4(g) → C9H20(g)
ΔH = -186 kJ/mol
Equation 2:
C9H20(g) + 14O2 → 10H2O(l) + 9CO2(g)
ΔH = -6171 kJ/mol
Equation 1b
C5H12(g) + 2C2H4(g) + C9H20(g) + 14O2 → C9H20(g) + 10H2O(l) + 9CO2(g)
ΔH = -186 -6171 = -6357 kJ/mol
Eliminating common terms:
Equation 1b:
C5H12(g) + 2C2H4(g) + 14O2 → 10H2O(l) + 9CO2(g)
ΔH = -6357 kJ/mol
Step 3: Eliminate C2H4(g) using Equation 3.
As in Equation 1b we have 2 moles of C2H4(g) on the left hand side and in Equation 3 we have 1 mol of C2H4(g) also on the left hand side, I multiply by 2 Equation 3 and reverse it (i.e. I multiply by -2), then I add both equations:
(-2)×Equation 3:
4H2O(l) + 4CO2(g) → 2C2H4(g) + 6O2
ΔH = -1411 ×(-2) = 2822 kJ/mol
Equation 1b:
C5H12(g) + 2C2H4(g) + 14O2 → 10H2O(l) + 9CO2(g)
ΔH = -6357 kJ/mol
Equation 1c:
4H2O(l) + 4CO2(g) + C5H12(g) + 2C2H4(g) + 14O2 → 2C2H4(g) + 6O2 + 10H2O(l) + 9CO2(g)
ΔH =2822 – 6357 = -3535 kJ/mol
Eliminating common terms, I start with the water
Equation 1c:
4H2O(l) + 4CO2(g) + C5H12(g) + 2C2H4(g) + 14O2 → 2C2H4(g) + 6O2 + 10H2O(l) + 9CO2(g)
ΔH = -3535 kJ/mol
Equation 1c:
4CO2(g) + C5H12(g) + 2C2H4(g) + 14O2 → 2C2H4(g) + 6O2 + 6H2O(l) + 9CO2(g)
ΔH = -3535 kJ/mol
Continue with the CO2:
Equation 1c:
4CO2(g) + C5H12(g) + 2C2H4(g) + 14O2 → 2C2H4(g) + 6O2 + 6H2O(l) + 9CO2(g)
ΔH = -3535 kJ/mol
Equation 1c:
C5H12(g) + 2C2H4(g) + 14O2 → 2C2H4(g) + 6O2 + 6H2O(l) + 5CO2(g)
ΔH = -3535 kJ/mol
We can remove the C2H4 in both sides:
Equation 1c:
C5H12(g) + 2C2H4(g) + 14O2 → 2C2H4(g) + 6O2 + 6H2O(l) + 5CO2(g)
ΔH = -3535 kJ/mol
Equation 1c:
C5H12(g) + 14O2 → 6O2 + 6H2O(l) + 5CO2(g)
ΔH = -3535 kJ/mol
And finally the O2.
Equation 1c:
C5H12(g) + 14O2 → 6O2 + 6H2O(l) + 5CO2(g)
ΔH = -3535 kJ/mol
Equation 1c:
C5H12(g) + 8 O2 → 6H2O(l) + 5CO2(g)
ΔH = -3535 kJ/mol
Leaving us with:
Equation 1c:
C5H12(g) + 8 O2 → 6H2O(l) + 5CO2(g)
ΔH = -3535 kJ/mol
And Equation 1c is the enthalpy change of combustion for pentane or Equation 4.
∆cH (C5H12(g)) = ……………………………… -3535…….. kJmol–1
[2]
(c)
Ethene can be produced from ethanol, as shown in Reaction 2 below.
C2H5OH(g) → C2H4(g) + H2O(g)
Reaction 2
(i)
Predict the sign of the entropy change, ∆S, for Reaction 2.
Explain your reasoning
The sign of the entropy change, ∆S, for Reaction 2 is expected to be positive.
This is because entropy is a measure of disorder or randomness in a system. In Reaction 2, ethanol (C₂H₅OH) in the gaseous state is converted into ethene (C₂H₄) and water (H₂O), both in the gaseous state. The number of gas molecules increases during the reaction, going from one molecule of ethanol to two molecules (ethene and water). This increase in the number of gas particles results in a greater distribution of energy and higher randomness in the system, leading to an overall increase in entropy.
[1]
(ii)
Reaction 2 is repeated:
C2H5OH(g) → C2H4(g) + H2O(g)
Reaction 2
The Gibbs equation is shown below.
∆G = ∆H – T∆S
The enthalpy change, ∆H, and the entropy change, ∆S, can be assumed to be constant at different temperatures.
Fig. 18.1 shows values of the free energy change, ∆G, in kJmol–1, at different temperatures, T, in K, for Reaction 2.
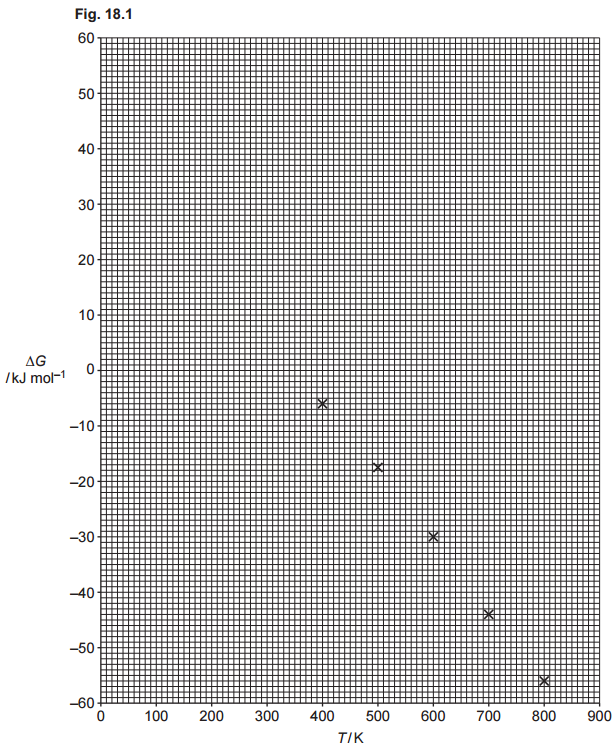
Use the graph in Fig. 18.1 to answer the following:
- Draw the best-fit line on the graph in Fig. 18.1.
- Determine ∆S, in JK–1mol–1, for Reaction 2.
- Determine the minimum temperature, T, at which the reaction is feasible.
- Determine ∆H for Reaction 2.
To ensure the best fit, use a ruler to draw a straight line that aligns as closely as possible with all the data points. Since the values derived from this line will be used in the rest of the exercise, it’s important to extend the line as far as possible—preferably until it intersects with the graph’s axes. If a ruler isn’t available, any tool that allows you to create a straight line will work just as well. I draw my line in red:
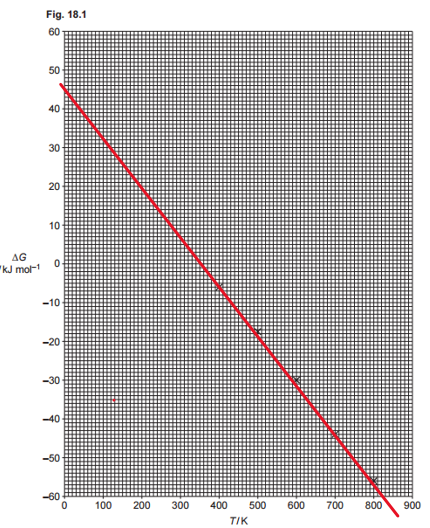
ΔS represents the slope of the line just drawn. To determine it accurately, select values that are spaced as far apart as possible. In this case, I chose points where the line intersects the axes. From the graph, when T = 0, ΔG = 45, and when ΔG = -60, T = 830. The slope can be calculated as:
$$
\small
\Delta S = \frac{\Delta(\Delta H)}{\Delta T} = \frac{[45 – (-60)]\,\mathrm{kJ\,mol^{-1}}}{830\,\mathrm{K}} = 0.127\,\mathrm{kJ\,K^{-1}\,mol^{-1}}
$$
Note that I have used the information that we have from the problem to calculate the value as positive. Now, watch up for the units, as the question asks for the answer in J K-1 mol-1, then the answer is 127 J K-1 mol-1.
The minimum temperature at which the reaction is feasible is when ΔG becomes negative. Using the line in the graph, we see that when ΔG=0 when the temperature is 350 K (or similar values, depending on your graph). At higher temperatures, ΔG<0, then the answer is 350 K:
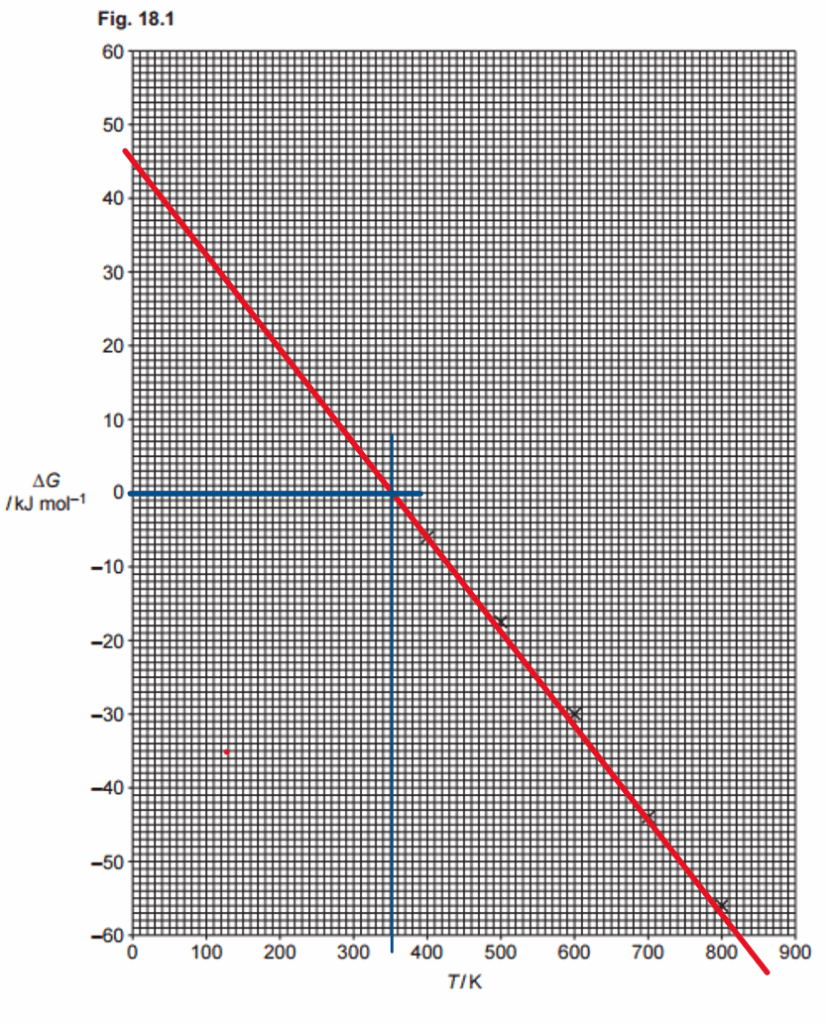
ΔH is the y-intercept. When T = 0, the value of ΔH = 45 kJ mol-1.
∆S = ………………………127……… JK–1mol–1
minimum T = ………………350….. K
∆H = …………………………45…… kJmol–1
[5]
